一、概論

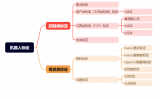
現(xiàn)在的機器人少不了有各種傳感器，傳感器之間的標(biāo)定是機器人感知環(huán)境的一個重要前提。所謂標(biāo)定，是指確定傳感器之間的坐標(biāo)轉(zhuǎn)換關(guān)系。由于標(biāo)定的傳感器各異，好像沒有特別通用的方法。

手眼標(biāo)定法是標(biāo)定攝像頭與機械臂的一個經(jīng)典方法，不過這個思想也適用于其他傳感器，比如自動駕駛中激光雷達與攝像頭之間的標(biāo)定，比如東京大學(xué)的這篇工作《LiDAR and Camera Calibration using Motion Estimated by Sensor Fusion Odometry》。

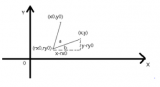
手眼標(biāo)定法的核心公式只有一個，??，這里的 X 就是指手（機械臂末端）與眼（攝像頭）之間的坐標(biāo)轉(zhuǎn)換關(guān)系。下面結(jié)合機械臂的兩種使用場景，講一下這個公式的由來。

用Base表示機械臂的底座（可以認為是世界坐標(biāo)系），用End表示機械臂的末端，用Camera表示攝像頭，用Object表示標(biāo)定板。

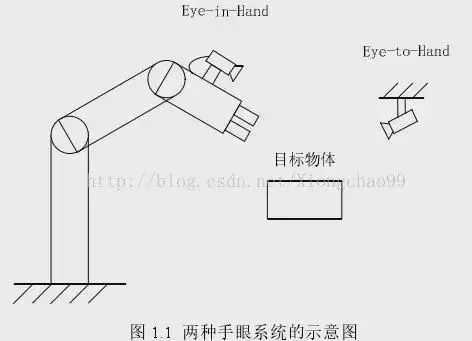
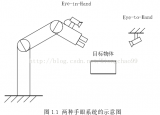
Eye-In-Hand

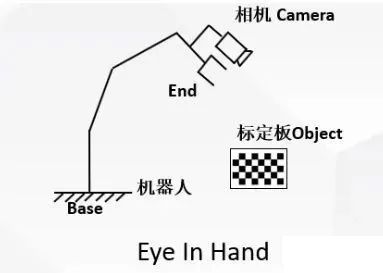
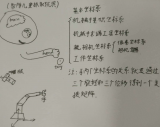
所謂Eye-In-Hand，是指攝像頭被安裝在機械臂上。此時要求取的是，End到Camera之間的坐標(biāo)轉(zhuǎn)換關(guān)系，也就是。這種情況下，有兩個變量是不變的：

攝像頭與機械臂末端之間的坐標(biāo)轉(zhuǎn)換關(guān)系不變，也就是說，??始終不變；

標(biāo)定板與機械臂底座之間的坐標(biāo)轉(zhuǎn)換關(guān)系不變，也就是說，??也是不變的。

把按照前后兩次運動展開，有

記

就得到了

也就是，如果能夠計算移動前后，機械臂末端的坐標(biāo)變換關(guān)系??以及相機的坐標(biāo)變換關(guān)系??，即可求出機械臂末端到相機之間的坐標(biāo)變換關(guān)系??。

Eye-To-Hand

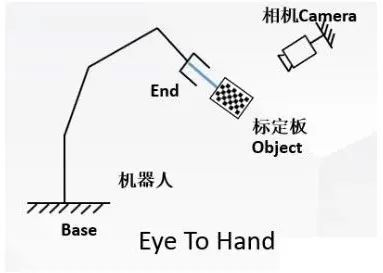
所謂Eye-To-Hand，是指攝像頭被安裝在一個固定不動的位置，而標(biāo)定板被拿在機械臂手上。此時要求取的是，Base到Camera之間的坐標(biāo)轉(zhuǎn)換關(guān)系，也就是。這種情況下，有兩個變量是不變的：

攝像頭與機械臂底座之間的坐標(biāo)轉(zhuǎn)換關(guān)系不變，也就是說，??始終不變；

標(biāo)定板與機械臂末端之間的坐標(biāo)轉(zhuǎn)換關(guān)系不變，也就是說，??始終不變。

把按照前后兩次運動展開，有

記

就得到了

本文主要是講解經(jīng)典手眼標(biāo)定問題中的TSAI-LENZ 文獻方法，參考文獻為“A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/Eye Calibration”，并且實現(xiàn)了基于OpenCV的C++代碼程序

二、Eye in hand 手眼標(biāo)定問題

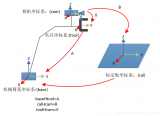
? ? ? ?在機器人校準(zhǔn)測量、機器人手眼協(xié)調(diào)以及機器人輔助測量等領(lǐng)域，都要求知道機器人執(zhí)行器末端（抓取臂）坐標(biāo)系和傳感器（比如用來測量三維空間中目標(biāo)位置和方向并固定在機器人手上的攝像機）坐標(biāo)系之間的相互關(guān)系，確定這種轉(zhuǎn)換關(guān)系在機器人領(lǐng)域就是通常所說的手眼標(biāo)定。

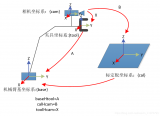
? ? ? ?將手眼標(biāo)定系統(tǒng)如下圖所示，其中Hgi為機器人執(zhí)行器末端坐標(biāo)系之間相對位置姿態(tài)的齊次變換矩陣；Hcij為攝像機坐標(biāo)系之間相對位置姿態(tài)的齊次變換矩陣；Hcg為像機與機器人執(zhí)行器末端之間的相對位置姿態(tài)齊次矩陣。

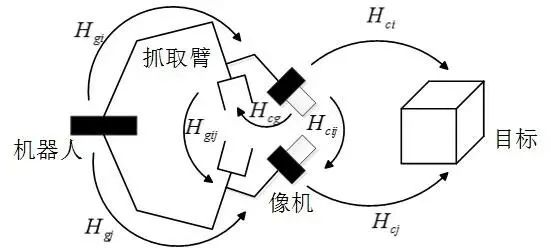
? ? ? ?經(jīng)過坐標(biāo)系變換，Hgij、Hcij和Hcg滿足上文所述的AX=XB關(guān)系：

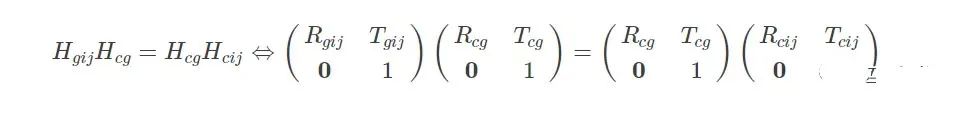
? ? ? ?將上式展開，可以得到手眼標(biāo)定的基本方程：

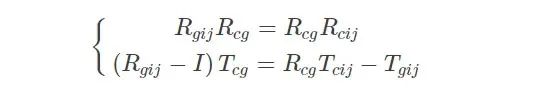
? ? ? ?因此，手眼標(biāo)定問題也就轉(zhuǎn)化為從上述方程組中求解出RcgRcg和TcgTcg，下面就按照TSAI文獻所述求解該方程組。

三、“兩步法”手眼標(biāo)定

? ? ? ?一般用“兩步法”求解基本方程，即先從基本方程上式求解出Rcg，再代入下式求解出Tcg。在TSAI文獻中引入旋轉(zhuǎn)軸-旋轉(zhuǎn)角系統(tǒng)來描述旋轉(zhuǎn)運動來進行求解該方程組，具體的公式推導(dǎo)可以查看原始文獻，這里只歸納計算步驟，不明白的地方可閱讀文獻，計算步驟如下：

Step1：利用羅德里格斯變換將旋轉(zhuǎn)矩陣轉(zhuǎn)換為旋轉(zhuǎn)向量

Step2：向量歸一化

Step3：修正的羅德里格斯參數(shù)表示姿態(tài)變化

Step4：計算初始旋轉(zhuǎn)向量P′cg

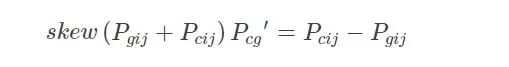
????其中，skew為反對稱運算，假設(shè)一個三維向量V=[vx;vy;vz]，其反對稱矩陣為：

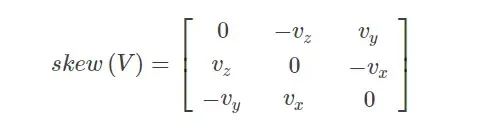
Step5：計算旋轉(zhuǎn)向量Pcg

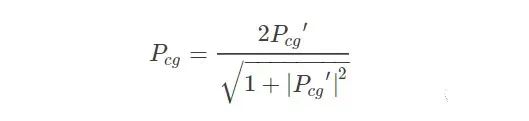
Step6：計算旋轉(zhuǎn)矩陣Rcg

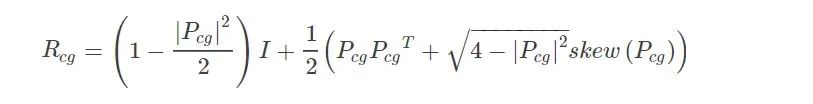
Step7：計算平移向量TcgTcg

四、MATLAB算法源代碼

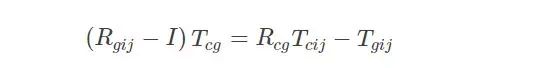
根據(jù)上述基本計算步驟，MATLAB實現(xiàn)代碼為：

代碼1：tsai函數(shù)（求解AX=XB）

?

function X = tsai(A,B)
% Calculates the least squares solution of
% AX = XB
% 
% A New Technique for Fully Autonomous 
% and Efficient 3D Robotics Hand/Eye Calibration
% Lenz Tsai
%
% Mili Shah
% July 2014


[m,n] = size(A); n = n/4;
S = zeros(3*n,3);
v = zeros(3*n,1);
%Calculate best rotation R
for i = 1:n
    A1 = logm(A(1:3,4*i-3:4*i-1)); 
    B1 = logm(B(1:3,4*i-3:4*i-1));
    a = [A1(3,2) A1(1,3) A1(2,1)]'; a = a/norm(a);
    b = [B1(3,2) B1(1,3) B1(2,1)]'; b = b/norm(b);
    S(3*i-2:3*i,:) = skew(a+b);
    v(3*i-2:3*i,:) = a-b;
end
x = Sv;
theta = 2*atan(norm(x));
x = x/norm(x);
R = (eye(3)*cos(theta) + sin(theta)*skew(x) + (1-cos(theta))*x*x')';
%Calculate best translation t
C = zeros(3*n,3);
d = zeros(3*n,1);
I = eye(3);
for i = 1:n
    C(3*i-2:3*i,:) = I - A(1:3,4*i-3:4*i-1);
    d(3*i-2:3*i,:) = A(1:3,4*i)-R*B(1:3,4*i);
end
t = Cd;
%Put everything together to form X
X = [R t;0 0 0 1];

?

代碼2：skew函數(shù)（求向量反對稱矩陣）

?

function Sk = skew( x )
%SKEW 此處顯示有關(guān)此函數(shù)的摘要
%   此處顯示詳細說明
   Sk = [0,-x(3),x(2);x(3),0,-x(1);-x(2),x(1),0];
end

?

代碼3：計算手眼矩陣Tm

?

clc
clear
close all


%%%%%%%%%%%%%%%%%%%%%%% T6矩陣參數(shù)%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%位姿1的時候機器人末端相對于機器人基坐標(biāo)系下變換矩陣
Pose1=[1141.243,-15.261,-97.721,178.91,0.47,92.37];
Px = Pose1(1);
Py = Pose1(2);
Pz = Pose1(3);
rota = Pose1(4)*pi/180;
rotb = Pose1(5)*pi/180;
rotc = Pose1(6)*pi/180;
Rx = [1 0 0; 0 cos(rota) -sin(rota); 0 sin(rota) cos(rota)];
Ry = [cos(rotb) 0 sin(rotb); 0 1 0; -sin(rotb) 0 cos(rotb)];
Rz = [cos(rotc) -sin(rotc) 0; sin(rotc) cos(rotc) 0; 0 0 1];
R1 = Rz*Ry*Rx;
T1= [Px Py Pz]';
%%%%%%%%%%位姿2的時候機器人末端相對于機器人基坐標(biāo)系下變換矩陣
Pose2=[1103.946,-163.910,-107.673,-160.90,-0.14,-91.62];
Px = Pose2(1);
Py = Pose2(2);
Pz = Pose2(3);
rota = Pose2(4)*pi/180;
rotb = Pose2(5)*pi/180;
rotc = Pose2(6)*pi/180;
Rx = [1 0 0; 0 cos(rota) -sin(rota); 0 sin(rota) cos(rota)];
Ry = [cos(rotb) 0 sin(rotb); 0 1 0; -sin(rotb) 0 cos(rotb)];
Rz = [cos(rotc) -sin(rotc) 0; sin(rotc) cos(rotc) 0; 0 0 1];
R2 = Rz*Ry*Rx;
T2= [Px Py Pz]';
%%%%%%%%%%位姿3的時候機器人末端相對于機器人基坐標(biāo)系下變換矩陣
Pose3=[1073.714,2.669,-142.448,-142.86,0.84,-178.55];
Px = Pose3(1);
Py = Pose3(2);
Pz = Pose3(3);
rota = Pose3(4)*pi/180;
rotb = Pose3(5)*pi/180;
rotc = Pose3(6)*pi/180;
Rx = [1 0 0; 0 cos(rota) -sin(rota); 0 sin(rota) cos(rota)];
Ry = [cos(rotb) 0 sin(rotb); 0 1 0; -sin(rotb) 0 cos(rotb)];
Rz = [cos(rotc) -sin(rotc) 0; sin(rotc) cos(rotc) 0; 0 0 1];
R3 = Rz*Ry*Rx;
T3= [Px Py Pz]';
%%%%%%%%%位姿1,2,3時候機器人末端相對于機器人基坐標(biāo)系下變換矩陣
T61=[R1 T1;0 0 0 1]   ;      
T62=[R2 T2;0 0 0 1];
T63=[R3 T3;0 0 0 1];


%%%%%%攝像機外參數(shù)矩陣（平面靶標(biāo)在攝像機坐標(biāo)系下表示）%%%%%%%%
Extrinsic1=[0.051678,-0.998634,0.007660,21.747985;
         -0.998617,-0.051600,0.010060,27.391246;
        -0.009651,-0.008169,-0.999920,319.071378];%%%3行4列矩陣
Extrinsic2=[0.014949,0.999738,0.017361,-35.869608 
        0.949779,-0.019626,0.312304,-20.701811
        0.312563,0.011821,-0.949823,306.463155];
Extrinsic3=[0.999176,0.039246,0.010343,-26.361812
        0.025037,-0.796606,0.603980,20.533884
        0.031943,-0.603223,-0.796933,318.110756];


%%%%%%%
TC1=[Extrinsic1; 0 0 0 1];     
TC2=[Extrinsic2; 0 0 0 1];
TC3=[Extrinsic3; 0 0 0 1];


TL1=inv(T61)*T62;
TL2=inv(T62)*T63;
 
TR1=TC1*inv(TC2);
TR2=TC2*inv(TC3);


A=[TL1,TL2]
B=[TR1,TR2]
X=?tsai(A,B)

?

結(jié)果如下：

?

A =
   -0.9976    0.0676   -0.0173 -146.8929    0.0535   -0.7980    0.6003 -165.7422
   -0.0697   -0.9488    0.3082  -43.6165    0.9483    0.2289    0.2197   44.2528
    0.0044    0.3087    0.9512   10.3295   -0.3127    0.5575    0.7690   21.0485
         0         0         0    1.0000         0         0         0    1.0000
B =
   -0.9975    0.0711   -0.0029  -11.6622    0.0544   -0.7855   -0.6164  177.7842
   -0.0663   -0.9443   -0.3223  104.2345    0.9515    0.2280   -0.2067   65.4536
   -0.0257   -0.3213    0.9466   21.3907    0.3029   -0.5753    0.7598   84.5619
         0         0         0    1.0000         0         0         0    1.0000
X =
   -0.9998    0.0187   -0.0076  -78.8694
   -0.0187   -0.9998   -0.0073   14.2711
   -0.0078   -0.0071    0.9999 -124.6709
         0         0         0    1.0000

?

五、C++算法源代碼

在利用OpenCV 2.0開源庫的基礎(chǔ)上，編寫Tsai手眼標(biāo)定方法的c++程序，其實現(xiàn)函數(shù)代碼如下：

代碼1：Tsai_HandEye函數(shù)，求解AX=XB

?

void Tsai_HandEye(Mat Hcg, vector Hgij, vector Hcij)
{
  CV_Assert(Hgij.size() == Hcij.size());
  int nStatus = Hgij.size();


  Mat Rgij(3, 3, CV_64FC1);
  Mat Rcij(3, 3, CV_64FC1);


  Mat rgij(3, 1, CV_64FC1);
  Mat rcij(3, 1, CV_64FC1);


  double theta_gij;
  double theta_cij;


  Mat rngij(3, 1, CV_64FC1);
  Mat rncij(3, 1, CV_64FC1);


  Mat Pgij(3, 1, CV_64FC1);
  Mat Pcij(3, 1, CV_64FC1);


  Mat tempA(3, 3, CV_64FC1);
  Mat tempb(3, 1, CV_64FC1);


  Mat A;
  Mat b;
  Mat pinA;


  Mat Pcg_prime(3, 1, CV_64FC1);
  Mat Pcg(3, 1, CV_64FC1);
  Mat PcgTrs(1, 3, CV_64FC1);


  Mat Rcg(3, 3, CV_64FC1);
  Mat eyeM = Mat::eye(3, 3, CV_64FC1);
    
  Mat Tgij(3, 1, CV_64FC1);
  Mat Tcij(3, 1, CV_64FC1);


  Mat tempAA(3, 3, CV_64FC1);
  Mat tempbb(3, 1, CV_64FC1);


  Mat AA;
  Mat bb;
  Mat pinAA;


  Mat Tcg(3, 1, CV_64FC1);


  for (int i = 0; i < nStatus; i++)
  {
    Hgij[i](Rect(0, 0, 3, 3)).copyTo(Rgij);
    Hcij[i](Rect(0, 0, 3, 3)).copyTo(Rcij);


    Rodrigues(Rgij, rgij);
    Rodrigues(Rcij, rcij);


    theta_gij = norm(rgij);
    theta_cij = norm(rcij);


    rngij = rgij / theta_gij;
    rncij = rcij / theta_cij;


    Pgij = 2 * sin(theta_gij / 2)*rngij;
    Pcij = 2 * sin(theta_cij / 2)*rncij;


    tempA = skew(Pgij + Pcij);
    tempb = Pcij - Pgij;


    A.push_back(tempA);
    b.push_back(tempb);
  }


  //Compute rotation
  invert(A, pinA, DECOMP_SVD);


  Pcg_prime = pinA * b;
  Pcg = 2 * Pcg_prime / sqrt(1 + norm(Pcg_prime) * norm(Pcg_prime));
  PcgTrs = Pcg.t();  
  Rcg = (1 - norm(Pcg) * norm(Pcg) / 2) * eyeM + 0.5 * (Pcg * PcgTrs + sqrt(4 - norm(Pcg)*norm(Pcg))*skew(Pcg));


  //Computer Translation 
  for (int i = 0; i < nStatus; i++)
  {
    Hgij[i](Rect(0, 0, 3, 3)).copyTo(Rgij);
    Hcij[i](Rect(0, 0, 3, 3)).copyTo(Rcij);
    Hgij[i](Rect(3, 0, 1, 3)).copyTo(Tgij);
    Hcij[i](Rect(3, 0, 1, 3)).copyTo(Tcij);


    tempAA = Rgij - eyeM;
    tempbb = Rcg * Tcij - Tgij;


    AA.push_back(tempAA);
    bb.push_back(tempbb);
  }


  invert(AA, pinAA, DECOMP_SVD);
  Tcg = pinAA * bb;


  Rcg.copyTo(Hcg(Rect(0, 0, 3, 3)));
  Tcg.copyTo(Hcg(Rect(3, 0, 1, 3)));
  Hcg.at(3, 0) = 0.0;
  Hcg.at(3, 1) = 0.0;
  Hcg.at(3, 2) = 0.0;
??Hcg.at(3,?3)?=?1.0;
}

?

代碼2：skew函數(shù)（將3x1向量轉(zhuǎn)換成3x3反對稱矩陣）

?

Mat skew(Mat A)
{
  CV_Assert(A.cols == 1 && A.rows == 3);
  Mat B(3, 3, CV_64FC1);


  B.at(0, 0) = 0.0;
  B.at(0, 1) = -A.at(2, 0);
  B.at(0, 2) = A.at(1, 0);


  B.at(1, 0) = A.at(2, 0);
  B.at(1, 1) = 0.0;
  B.at(1, 2) = -A.at(0, 0);


  B.at(2, 0) = -A.at(1, 0);
  B.at(2, 1) = A.at(0, 0);
  B.at(2, 2) = 0.0;


  return B;
}

?

代碼3：計算手眼矩陣Tm

?

#include??//頭文件
#include 
#include 
#include 
using namespace std;
using namespace cv; //包含cv命名空間
int?main()
{
    double a1[4][4] = { -0.9976,0.0676, - 0.0173, - 146.8929,
      -0.0697 ,- 0.9488 ,   0.3082 ,- 43.6165,
      0.0044 ,    0.3087,    0.9512 ,  10.3295,
      0 ,   0  ,   0 ,  1.0000 };
    double a2[4][4] = { 0.0535, - 0.7980,    0.6003 ,-165.7422,
      0.9483 , 0.2289, 0.2197, 44.2528,
      -0.3127,0.5575,0.7690, 21.0485,
      0, 0, 0, 1 };
  
    double b1[4][4] = { -0.9975,  0.0711, - 0.0029 ,- 11.6622,
      -0.0663, - 0.9443, - 0.3223,  104.2345,
      -0.0257, - 0.3213,    0.9466 ,  21.3907,
      0, 0, 0, 1 };
    double b2[4][4] = { 0.0544, - 0.7855, - 0.6164,  177.7842,
      0.9515,    0.2280 ,- 0.2067,   65.4536,
      0.3029, - 0.5753,    0.7598 ,  84.5619,
      0, 0, 0, 1 };
  
    Mat A1(4, 4, CV_64FC1, a1);
    Mat A2(4, 4, CV_64FC1, a2);
    Mat B1(4, 4, CV_64FC1, b1);
    Mat B2(4, 4, CV_64FC1, b2);
  
    vector Hgij;
    vector Hcij;
  
    Hgij.push_back(A1);
    Hgij.push_back(A2);
    Hcij.push_back(B1);
    Hcij.push_back(B2);
  
    Mat Hcg1(4, 4, CV_64FC1);
    Tsai_HandEye(Hcg1, Hgij, Hcij);
}

?

輸出結(jié)果如下：

?

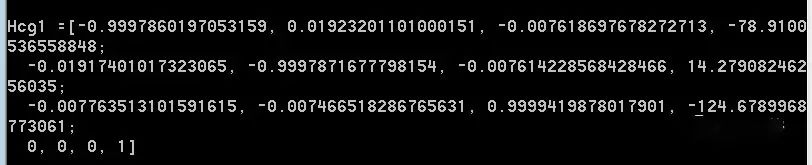
　　審核編輯：湯梓紅