一、關聯算法簡介
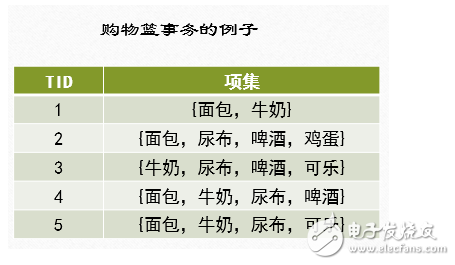
關聯規則的目的在于在一個數據集中找出項之間的關系,也稱之為購物藍分析 (market basketanalysis)。例如,購買鞋的顧客,有10%的可能也會買襪子,60%的買面包的顧客,也會買牛奶。這其中最有名的例子就是“尿布和啤酒”的故事了。關聯規則的應用場合。在商業銷售上,關聯規則可用于交叉銷售,以得到更大的收入;在保險業務方面,如果出現了不常見的索賠要求組合,則可能為欺詐,需要作進一步的調查。在醫療方面,可找出可能的治療組合;在銀行方面,對顧客進行分析,可以推薦感興趣的服務等等。Apriori algorithm是關聯規則里一項基本算法。
二、關聯算法的基本原理
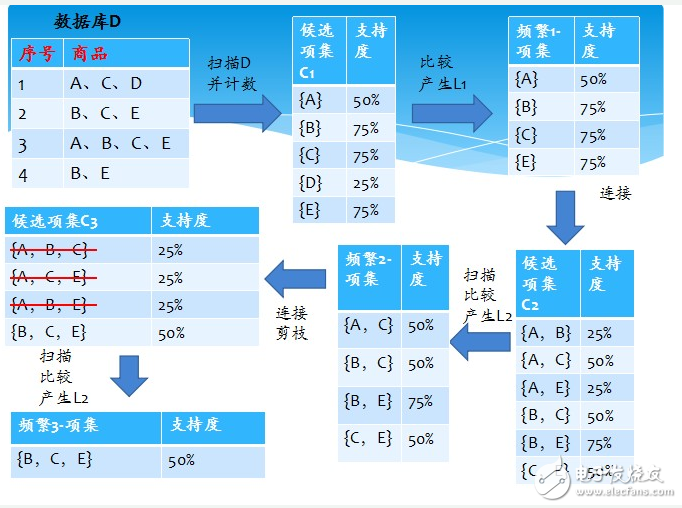
該算法的基本思想是:首先找出所有的頻集,這些項集出現的頻繁性至少和預定義的最小支持度一樣。然后由頻集產生強關聯規則,這些規則必須滿足最小支持度和最小可信度。然后使用第1步找到的頻集產生期望的規則,產生只包含集合的項的所有規則,其中每一條規則的右部只有一項,這里采用的是中規則的定義。一旦這些規則被生成,那么只有那些大于用戶給定的最小可信度的規則才被留下來。為了生成所有頻集,使用了遞推的方法
?
三、關聯算法的C++簡單實現
(1)算法數據:
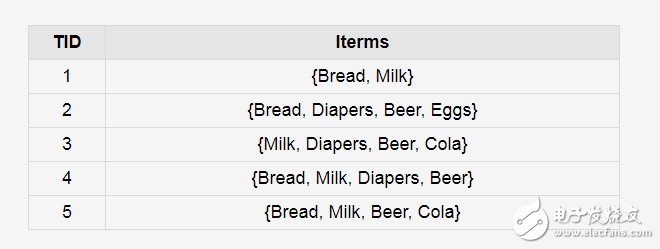
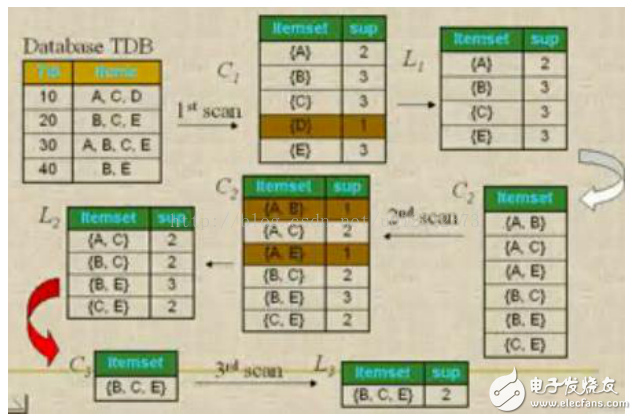
對給定數據集用Apriori算法進行挖掘,找出其中的頻繁集并生成關聯規則。對下面數據集進行挖掘:
?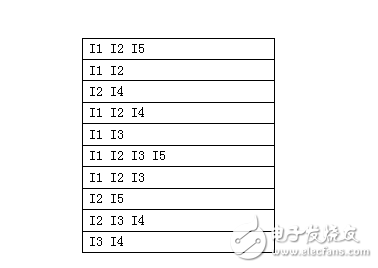
對于數據集,取最小支持度minsup=2,最小置信度minconf=0.8。
(2)算法步驟:
① 首先單趟掃描數據集,計算各個一項集的支持度,根據給定的最小支持度閔值,得到一項頻繁集L1。
② 然后通過連接運算,得到二項候選集,對每個候選集再次掃描數據集,得出每個候選集的支持度,再與最小支持度比較。得到二項頻繁集L2。
③ 如此進行下去,直到不能連接產生新的候選集為止。
④ 對于找到的所有頻繁集,用規則提取算法進行關聯規則的提取。
(3)C++算法的簡單實現
①首先要在工程名文件夾里自己定義date.txt文檔存放數據,然后在main函數中用FILE* fp=fopen(“date.txt”,“r”);將數據導入算法。
②定義int countL1[10];找到各一維頻繁子集出現的次數。
定義char curL1[20][2];實現出現的一維子集。
由于給出的數據最多有4個數,所以同樣的我們要定義到4維來放數據。
int countL2[10]; //各二維頻繁子集出現的次數
char curL2[20][3]; //出現的二維子集
int countL3[10]; //各三維頻繁子集出現的次數
char curL3[20][4]; //出現的三維子集
char cur[50][4];
③定義int SizeStr(char* m) 得到字符串的長度。實現代碼如下:
int SizeStr(char* m)
{
int i=0;
while(*(m+i)!=0)
{
i++;
}
return i;
}
④比較兩個字符串,如果相等返回true,否則返回false
bool OpD(char* x,char* y)
{
int i=0;
if(SizeStr(x)==SizeStr(y))
{
while(*(x+i)==*(y+i))
{
i++;
if(*(x+i)==0 && *(y+i)==0)
return true;
}
}
return false;
}
⑤通過void LoadItemL1(char **p) 得到所有1元的字串和各自出現的次數
void LoadItemL1(char **p)
{
int i,j,n=0,k=0;
char ch;
char* s;
int f;
memset(cur,0,sizeof(cur));
for(i=0;i《20;i++)
{
curL1[i][0]=0;
curL1[i][1]=0;
}
for(j=0;j《10;j++)
countL1[j]=0;
for(i=0;i《10;i++)
for(j=0;j《4;j++)
{
ch=*(*(p+i)+j);
if(ch==0)
break;
cur[n][0]=ch;
n++;
}
curL1[0][0]=cur[0][0];
curL1[0][1]=cur[0][1];
k=0;
for(i=0;i《50;i++)
{
if(cur[i]==0)
break;
s=cur[i];
f=1;
for(j=0;j《=k;j++)
{
if(OpD(s,curL1[j]))
{
f=0;
break;
}
}
if(f==1)
{
++k;
curL1[k][0]=cur[i][0];
curL1[k][1]=cur[i][1];
}
}
for(i=0;i《20;i++)
for(j=0;j《50;j++)
{
char* m;
m=curL1[i];
if(*m==0)
break;
if(OpD(m,cur[j]))
countL1[i]++;
}
printf(“L1: \n ”);
printf(“項集 支持度計數\n”);
for(i=0;i《10;i++)
{
if(curL1[i]==0)
break;
if(countL1[i]》=2)
printf(“{I%s}: %d\n”,curL1[i],countL1[i]);
}
}
⑥通過void SubItem2(char **p) 得到所有的2元子串
void SubItem2(char **p)
{
int i,j,k,n=0;
char* s;
memset(cur,0,sizeof(cur));
for(i=0;i《20;i++)
{
curL2[i][0]=0;
curL2[i][1]=0;
curL2[i][2]=0;
}
for(i=0;i《10;i++)
countL2[i]=0;
for(k=0;k《10;k++)
{
s=*(p+k);
if(SizeStr(s)《2)
continue;
for(i=0;i《SizeStr(s);i++)
for(j=i+1;j《SizeStr(s);j++)
{
if(*(s+j)==0)
break;
*(cur[n]+0)=*(s+i);
*(cur[n]+1)=*(s+j);
*(cur[n]+2)=0;
*(cur[n]+3)=0;
n++;
}
}
}
⑦通過void LoadItemL2(char **p) 得到各個2元頻繁子串出現的次數
void LoadItemL2(char **p)
{
int k,i,j;
char* s;
int f;
SubItem2(p);
curL2[0][0]=cur[0][0];
curL2[0][1]=cur[0][1];
curL2[0][2]=cur[0][2];
k=0;
for(i=0;i《50;i++)
{
if(cur[i]==0)
break;
s=cur[i];
f=1;
for(j=0;j《=k;j++)
{
if(OpD(s,curL2[j]))
{
f=0;
break;
}
}
if(f==1)
{
++k;
curL2[k][0]=cur[i][0];
curL2[k][1]=cur[i][1];
curL2[k][2]=cur[i][2];
}
}
for(i=0;i《20;i++)
for(j=0;j《50;j++)
{
s=curL2[i];
if(*s==0)
break;
if(OpD(s,cur[j]))
countL2[i]++;
}
printf(“L2: \n”);
printf(“項集 支持度計數\n”);
for(i=0;i《10;i++)
{
if(curL2[i]==0)
break;
if(countL2[i]》=2)
printf(“{I%c,I%c}: %d\n”,curL2[i][0],curL2[i][1],countL2[i]);
}
}
⑧通過定義void SubItem3(char **p) 得到所有3元的子串
void SubItem3(char **p)
{
char *s;
int i,j,h,m;
int n=0;
memset(cur,0,sizeof(cur));
for(j=0;j《20;j++)
{
curL3[j][0]=0;
curL3[j][1]=0;
curL3[j][2]=0;
curL3[j][3]=0;
}
for(i=0;i《10;i++)
countL3[i]=0;
for(m=0;m《10;m++)
{
s=*(p+m);
if(SizeStr(s)《3)
continue;
for(i=0;i《SizeStr(s);i++)
for(j=i+1;j《SizeStr(s);j++)
{
for(h=j+1;h《SizeStr(s);h++)
{
if(*(s+h)==0)
break;
*(cur[n]+0)=*(s+i);
*(cur[n]+1)=*(s+j);
*(cur[n]+2)=*(s+h);
*(cur[n]+3)=0;
n++;
}
}
}
}
⑨同樣我們要得到得到各個3元頻繁子串出現的次數
void LoadItemL3(char** p)
{
int k,i,j;
char* s;
int f;
SubItem3(p);
curL3[0][0]=cur[0][0];
curL3[0][1]=cur[0][1];
curL3[0][2]=cur[0][2];
curL3[0][3]=cur[0][3];
k=0;
for(i=0;i《50;i++)
{
if(cur[i]==0)
break;
s=cur[i];
f=1;
for(j=0;j《=k;j++)
{
if(OpD(s,curL3[j]))
{
f=0;
break;
}
}
if(f==1)
{
++k;
curL3[k][0]=cur[i][0];
curL3[k][1]=cur[i][1];
curL3[k][2]=cur[i][2];
curL3[k][3]=cur[i][3];
}
}
for(i=0;i《20;i++)
for(j=0;j《50;j++)
{
s=curL3[i];
if(*s==0)
break;
if(OpD(s,cur[j]))
countL3[i]++;
}
printf(“L3: \n”);
printf(“項集 支持度計數\n”);
for(i=0;i《10;i++)
{
if(curL3[i]==0)
break;
if(countL3[i]》=2)
printf(“{I%c,I%c,I%c}: %d\n”,curL3[i][0],curL3[i][1],curL3[i][2],countL3[i]);
}
}
⑩定義void LoadItemL4(char** p) 得到各個3元子串出現的次數
void LoadItemL4(char** p)
{
int i;
char* s;
int j=0;
for(i=0;i《10;i++)
{
s=*(p+i);
if(SizeStr(s)==4)
j++;
}
printf(“四維子集出現的次數: %d\n”,j);
printf(“沒有四維的頻繁子集,算法結束! \n”);
}
11通過void Support(char* w,int g) 得到關聯規則,并輸出結果
void Support(char* w,int g)
{
int i,j,k,n=0;
char* s;
float c=0.8,d=0;
memset(cur,0,sizeof(cur));
s=w;
for(i=0;i《SizeStr(s);i++)
{
*(cur[n]+0)=*(s+i);
*(cur[n]+1)=0;
*(cur[n]+2)=0;
*(cur[n]+3)=0;
n++;
}
for(i=0;i《SizeStr(s);i++)
for(j=i+1;j《SizeStr(s);j++)
{
if(*(s+j)==0)
break;
*(cur[n]+0)=*(s+i);
*(cur[n]+1)=*(s+j);
*(cur[n]+2)=0;
*(cur[n]+3)=0;
n++;
}
for(i=0;i《10;i++)
{
if(SizeStr(cur[i])==1)
{
for(j=0;j《10;j++)
{
if(OpD(cur[i],curL1[j]))
{
d=countL3[g]/(float)countL1[j];
if(d》=c)
printf(“{I%s}: %f”,curL1[i],d);
break;
}
}
}
if(SizeStr(cur[i])==2)
{
for(j=0;j《10;j++)
{
if(OpD(cur[i],curL2[j]))
{
d=countL3[g]/(float)countL2[j];
if(d》=c)
printf(“{I%c,I%c}: %f \n”,curL2[j][0],curL2[j][1],d);
break;
}
}
}
}
}
12最后通過main函數完成整過程序
int main(int argc, char* argv[])
{
int i=0,j=0,k;
char buf[10][6];
char* p[10];
char ch;
memset(buf,0,sizeof(buf));
FILE* fp=fopen(“date.txt”,“r”);
if(fp==NULL)
return 0;
ch=fgetc(fp);
while(ch!=EOF)
{
if(ch==0xa || ch==0xd)
{
i++;
ch=fgetc(fp);
j=0;
continue;
}
buf[i][j]=ch;
j++;
ch=fgetc(fp);
}
for(k=0;k《10;k++)
{
*(p+k)=buf[k];
}
LoadItemL1(p);
LoadItemL2(p);
LoadItemL3(p);
LoadItemL4(p);
printf(“產生關聯規則: \n”);
printf(“非空子集: 置信度:\n”);
for(i=0;i《10;i++)
{
if(curL3[i]!=0 && countL3[i]》=2)
Support(curL3[i],i);
}
return 0;
}
(4)程序輸出結果:
四、學習心得體會
關聯算法基本原理學習思路簡單,只需一步一步找出頻集。再通過支持度算出可信度,如對于A—》C,support=support({A,C}),confidence= support({A,C})/support({A})。其中頻繁子集的任何子集一定是頻繁的,子集頻繁父親一定頻繁。相對較難的的部分在于C++代碼的實現部分依次實現各個頻繁子集,完成整個程序。這學期在商務智能課中學習了數據挖掘的10大算法,數據挖掘十分經典,掌握好一個簡單的算法要下很功夫,在今后的工作中一定可以用到,我很慶幸這學期能選到這個課,在這之前聽說過數據挖掘但一直沒有機會接觸,原理容易理解但沒接觸到以前就沒有想過這樣考慮問題,學習這個課程以后無論是知識面,智力上都是一個跳躍。還有也提醒我要多復習C++問題的思考,這學期一直忙于網頁編程,忘記了上學期說要復習C++數據結構的學習。希望以后還有機會能選到老師的課。
 電子發燒友App
電子發燒友App









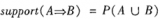










評論