根據(jù)數(shù)學模型的相似原理,我們應用電子元件模擬工程系統(tǒng)中的典型環(huán)節(jié),然后加入典型測試信號,測試環(huán)節(jié)的輸出響應。反之從實測的輸出響應也可以求得未知環(huán)節(jié)的傳遞函數(shù)及其各個參數(shù)。
模擬典型環(huán)節(jié)傳遞函數(shù)的方法有兩種:第一種方法,利用模擬裝置中的運算部件,采用逐項積分法,進行適當?shù)慕M合,構成典型環(huán)節(jié)傳遞函數(shù)模擬結構圖;第二種方法將運算放大器與不同的輸入網(wǎng)絡、反饋網(wǎng)絡組合,構成傳遞函數(shù)模擬線路圖,這種方法可以稱為復合網(wǎng)絡法。本節(jié)介紹第二種方法。
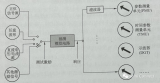
| (a)模擬電路 | (b)輸出響應 |
| 圖2-3-1慣性環(huán)節(jié)的模擬電路及響應 |
當輸入負階躍信號時,其輸出響應如圖2-3-1(b)所示。從圖中可知,T和K是響應曲線的兩個特征量。T表示階躍信號輸入后,響應按指數(shù)上升的快慢,它可從響應曲線實測得到。

 |
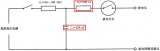
| (a)模擬電路 | (b)輸出響應 |
| 圖2-3-2 積分環(huán)節(jié)的模擬電路及響應 |
當輸入負階躍信號時,其輸出響應如圖2-3-2(b)所示。從圖中可知,積分時間常數(shù)Ti是積分環(huán)節(jié)的特征量,它表示階躍輸入后響應按線性上升的快慢,Ti可從響應曲線上求出,即響應上升到階躍輸入幅值時所需的時間。積分環(huán)節(jié)的特點是,不管輸入幅值多小,輸出就不斷地按線性增長,輸入幅值愈小,增長的速率愈小,只有輸入為零時,輸出才停止增長而保持其原來的數(shù)值。從圖中可看出運算放大器最終達到飽和值。
| (a)模擬電路 | (b)輸出響應 |
| 圖2-3-3 比例積分環(huán)節(jié)的模擬電路及響應 |
當輸入負階躍信號時,其輸出響應如圖2-3-3(b)所示。從該圖中可以得到比例積分環(huán)節(jié)的特征參數(shù)K和Ti。必須注意:在測試積分環(huán)節(jié)和比例積分環(huán)節(jié)的階躍響應時,由于存在儲能元件C,因此每次輸入階躍響應時,必須保證uc為零,否則將因uc的初始值不同使每次測得的響應不同。
| (a)模擬電路 | (b)輸出響應 |
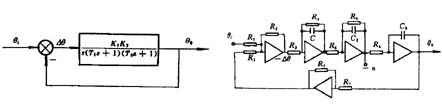
| 圖2-3-4 比例積分微分環(huán)節(jié)的模擬電路及理想的響應 |
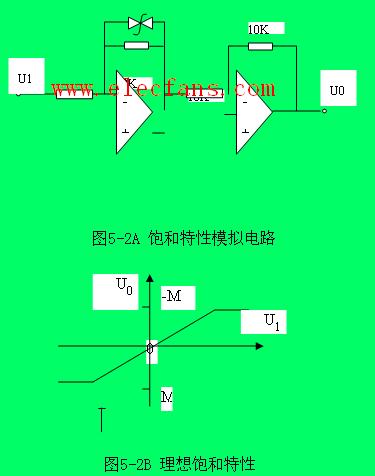
對于理想的比例積分微分環(huán)節(jié),當輸入負階躍信號時其輸出響應如圖2-3-4(b)所示,在輸入躍變時,它的輸出響應能夠以無限大的變化率在瞬間躍至∞ ,又在此瞬間下降至按某一比例Kp分配的電壓值,并立即按積分時間常數(shù)Ti規(guī)律線性增長。而模擬比例積分微分環(huán)節(jié)的輸出響應,在輸入躍變時只能以有限的變化率上升至運算放大的飽和值就不再增長,經(jīng)過一段時間,又以有限的變化率下降。這是因為模擬電路是在滿足R1>>R3 、C21>>C1 的條件下,忽略了小時間常數(shù)才得到近似的PID數(shù)學模型式,而且運算放大器也不是理想的,因此實際比例積分微分環(huán)節(jié)的響應曲線與圖2-3-4(b)略有不同。
綜上所述,典型環(huán)節(jié)的模擬方法是:根據(jù)典型環(huán)節(jié)的傳遞函數(shù),選擇適當?shù)木W(wǎng)絡作為運算放大器的輸入阻抗與反饋阻抗,使模擬電路的傳遞函數(shù)與被模擬環(huán)節(jié)的傳遞函數(shù)具有同一表達式,然后根據(jù)被模擬環(huán)節(jié)傳遞函數(shù)的參數(shù),計算出模擬電路各元件的參數(shù)值。
 電子發(fā)燒友App
電子發(fā)燒友App































評論