模型的可解釋性是機器學習領域的一個重要分支,隨著 AI 應用范圍的不斷擴大,人們越來越不滿足于模型的黑盒特性,與此同時,金融、自動駕駛等領域的法律法規也對模型的可解釋性提出了更高的要求,在可解釋 AI 一文中我們已經了解到模型可解釋性發展的相關背景以及目前較為成熟的技術方法,本文通過一個具體實例來了解下在 MATLAB 中是如何使用這些方法的,以及在得到解釋的數據之后我們該如何理解分析結果。
?
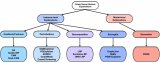
要分析的機器學習模型
?
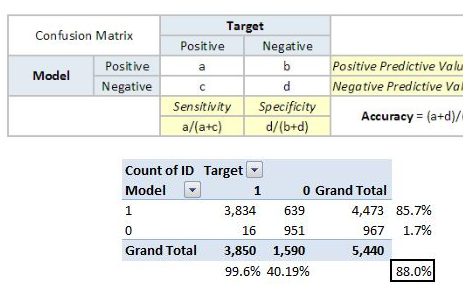
我們以一個經典的人體姿態識別為例,該模型的目標是通過訓練來從傳感器數據中檢測人體活動。傳感器數據包括三軸加速計和三軸陀螺儀共6組數據,我們可以通過手機或其他設備收集,訓練的目的是識別出人體目前是走路、站立、坐、躺等六種姿態中的哪一種。我們將收集到的數據做進一步統計分析,如求均值和標準差等,最終獲得18組數據,即18個特征。然后可以在 MATLAB 中使用分類學習器 App 或者通過編程的形式進行訓練,訓練得到的模型混淆矩陣如下,可以看到對于某些姿態的識別,模型會存在一定誤差。那么接下來我們就通過一系列模型可解釋性的方法去嘗試解讀一下錯誤判別的來源。
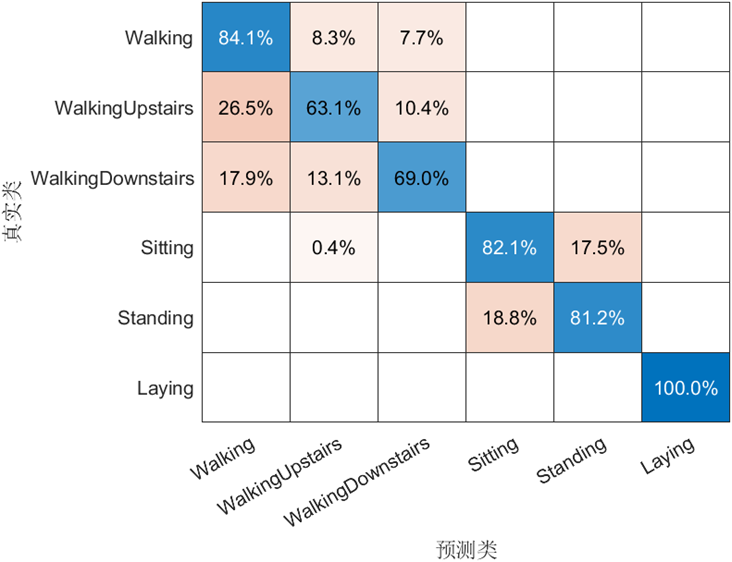
從混淆矩陣中可以看到,模型對于躺 ‘Laying’ 的姿態識別率為 100%,而對于正常走路和上下樓這三種 ‘Walking’ 的姿態識別準確率較低,尤其是上樓和下樓均低于70%。這也符合我們的預期,因為躺的姿態和其他差別較大,而幾種走路之間差異較小。
但我們也留意到模型在 ‘Sitting’ 和 ‘Standing’ 之間也產生了較大的誤差,考慮到這兩者之間的差異,我們想探究一下產生這種分類錯誤背后的原因。首先我們從圖中所示的區域選擇了一個樣本點 query point,該樣本的正確姿態為 ‘Sitting’,但是模型識別成了 ‘Standing’,為便于下一步分析,這里將該樣本點所有特征及其取值列舉了出來,如前所述一共 18 個,分別對應于原始的6個傳感器數據的平均值、標準差以及第一主成分:
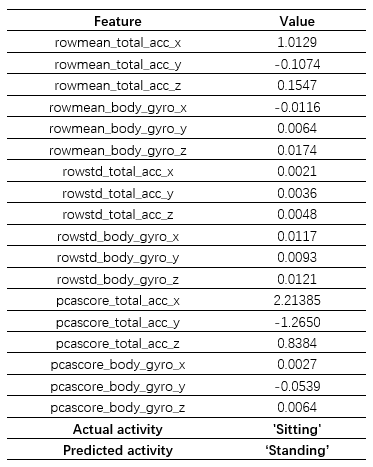
使用可解釋性方法進行分析
模型可解釋性分析的目的在于嘗試對機器學習黑盒模型的預測結果給出一個合理的解釋,定性地反映出輸入數據的各個特征和預測結果之間的關系。對于預測正確的結果,我們可以判斷預測過程是否符合我們基于領域知識對該問題的理解,是否有一些偶然因素導致結果碰巧正確,從而保證了模型可以在大規模生產環境下做進一步應用,也可以滿足一些法規的要求。
而對于錯誤的結果,如上文中的姿態識別,我們可以通過可解釋性來分析錯誤結果是由哪些因素導致的,更具體地說,即上述 18 個特征對結果的影響。在此基礎上,可以更有針對性地進行特征選擇、參數優化等模型改進工作。
接下來我們就嘗試用幾種不同的可解釋性方法來對上文中的 query point 做進一步分析,希望可以找到一些模型分類錯誤的線索。
2.1 Shapley 值
我們嘗試的第一個方法是 Shapley 值,Shapley 值起源于合作博弈理論,它基于嚴格的理論分析并給出了完整的解釋。作為一個局部解釋方法,Shapley 值通過對所有可能的特征組合依次計算,從而得到每個特征對預測結果的平均邊際貢獻,并且這些值是相對于該分類的平均得分而言的。可以簡單理解為邊際貢獻的分值越高,對產生當前預測結果的影響越大。因為有著完善的理論基礎且發展時間較長,Shapley 值被廣泛應用于金融領域來滿足一些法律法規的要求。
在 MATLAB 中使用 Shapley 值的方法也非常簡單,具體代碼如下:
exp = shapley(model,humanActivityDataTest,'QueryPoint',queryPt,'MaxNumSubsets',400);
plot(exp)
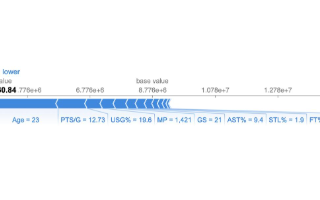
其中 shapley 即我們要調用的函數,函數的輸入依次是訓練好的模型,測試時完整的數據集,上文中要探測的樣本點 query point。值得一提的是,由于嚴格的 Shapley 值計算過程中需要對所有可能的特征組合依次計算,計算時間隨特征數量呈指數增長,所以我們在調用時設置了控制計算時間的 Subsets 參數。函數的輸出 exp 是結構體的形式,可以直接使用 plot 進行繪制,結果如下圖:
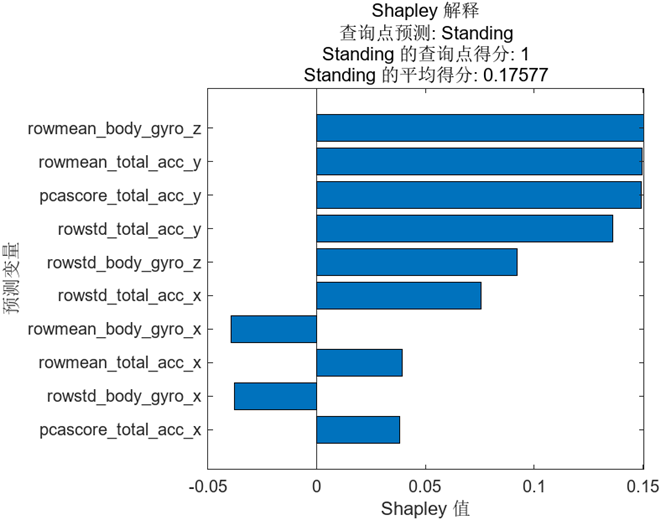
圖中按照 Shapley 值的絕對值大小依次進行了排序,那么該如何理解這些值即圖中所示的得分的含義呢?
我們之前已經了解到 Shapley 值反應的是每個特征的平均邊際貢獻,并且這些值是相對于該分類的平均得分而言的。首先需要計算出 ‘Standing’ 的平均得分,我們會將數據集中所有點關于 ‘Standing’ 的預測得分取平均得到相應的值,即 0.17577。而我們關注的樣本點預測為 ‘Standing’ 的得分為 1,相對較高,它和所有點的平均值相比差值為 0.82423,Shapley 值反應的正是該樣本點中每個特征對這個差值的貢獻,其總和也正是 0.82423。
圖中顯示了排行前十的特征及對應的 Shapley 值,我們可以看到 rowmean_body_gyro_z 的值最大,說明它對錯誤判別的影響最大,當然緊隨其后的幾個特征的 Shapley 值也較為接近。
特征 rowmean_body_gyro_z的實際含義為z方向陀螺儀的平均值,為什么這個特征可能導致了錯誤的結果?我們可以接著往下分析。
2.2 PDP - Partial Dependency Plot
Shapley 值雖然很清晰地給出了各個特征對于最終預測結果的貢獻,但是我們需要更多的信息來分析錯誤產生的來源,一個有效的方法是結合 PDP 又稱部分依賴圖來進行查看。
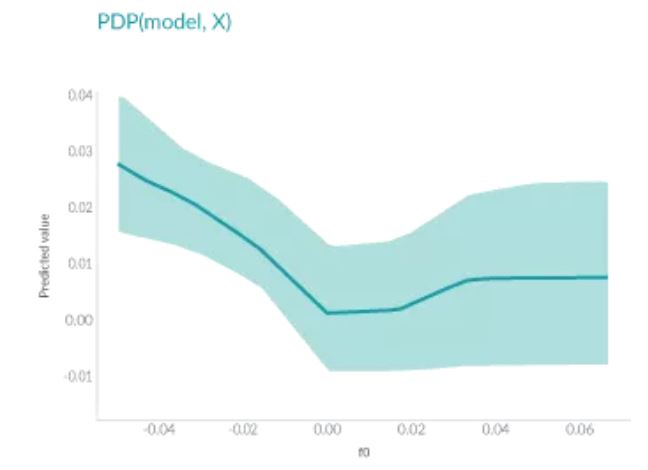
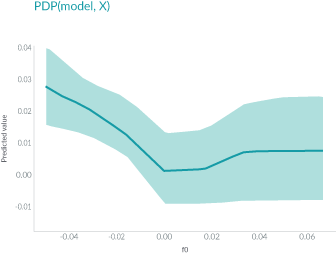
PDP 是一個全局解釋方法,關注單個特征對某一預測結果的整體影響,其思想是假設所有樣本中的該特征等于某一個固定值,從而計算出一個預測結果的平均值。當我們將該特征取一系列值時(取值范圍仍然來源于樣本),便可以繪制出對應的曲線。我們接著 Shapley 值的分析選擇特征 rowmean_body_gyro_z(對應數據中的位置為第6個特征),以及 query point 對應的真實分類 ‘Sitting’ 和錯誤分類 ‘Standing’ 分別繪制 PDP,在 MATLAB 中使用的方法仍然非常簡單,具體代碼及對應結果如下:
plotPartialDependence(model,6,'Sitting');
% rowmean_body_gyro_zis the 6th predictor in our data table
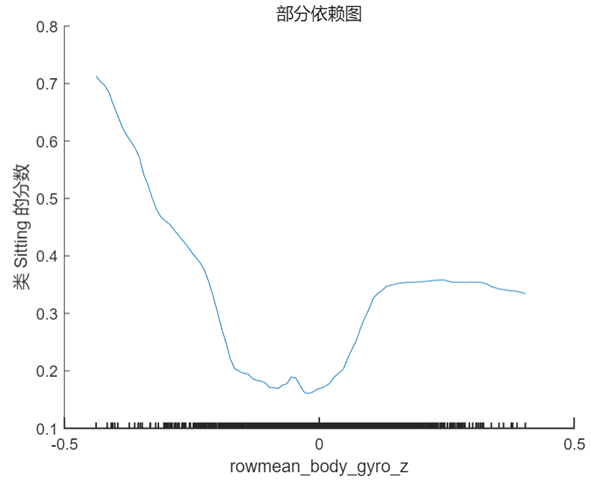
plotPartialDependence(model,6,'Standing');
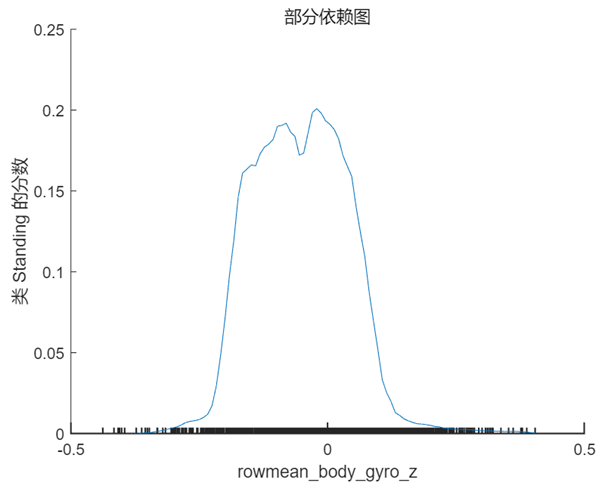
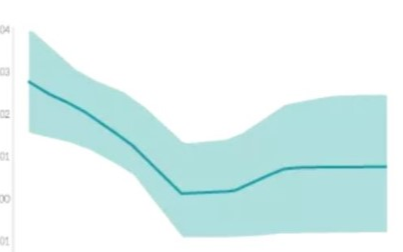
根據上圖以及第 1 節中 query point 在該特征的實際取值 0.017 可以看出,當該特征的取值接近于 0 時,分類為 ‘Standing’ 的分數較高,而當取值向兩端靠攏尤其是接近于 -0.5 時分類為 ‘sitting’ 的分數較高,甚至大于 0.5,這也符合該點的實際預測值。
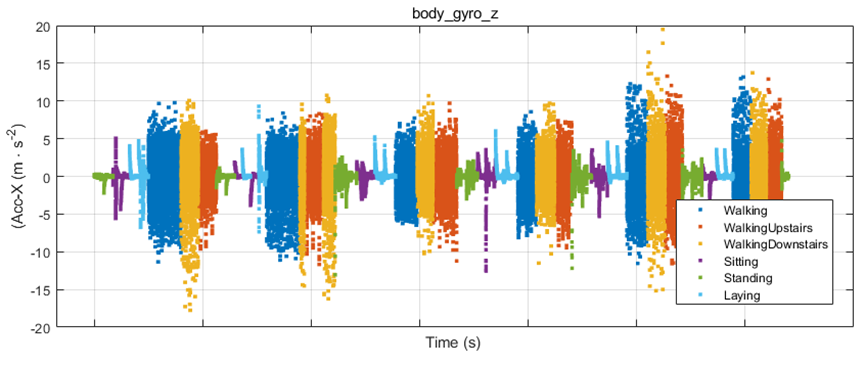
為了驗證上述分析結果,我們繪制了一部分樣本點(約 1000 個)body_gyro_z 的實際取值,結果如下圖所示,可以看到 ‘Sitting’(圖中紫色數據)的整體趨勢確實比 ‘Standing’(圖中綠色數據)要小一些,這說明了模型的訓練及預測過程是合理的。但兩者的差別并不大,而且對于單個的樣本點,比如我們現在關注的 query point,取值可能更大或者更小,并不符合大多數樣本的整體趨勢,這也是預測結果中個別樣本分類錯誤的原因之一。
通過部分依賴圖我們對 Shapley 值的分析結果有了更清楚的認識,雖然該樣本點的預測結果是錯誤的,但結合原始數據可以看出,這樣的結果是有跡可循且合理的。
在討論下一步工作之前,我們再嘗試一個新的可解釋性方法。
2.3 LIME - Local Interpretable Model-Agnostic Explanations
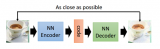
除了 Shapley 值,LIME 是另外一個應用廣泛的局部解釋方法,其簡單易理解,基本思想是針對關注的樣本點,在附近范圍內生成擾動數據并用黑盒模型獲得對應的預測結果,然后使用這些數據訓練出一個局部近似的可解釋模型,通過該模型幫助分析原始機器學習模型的預測過程。MATLAB 中可以使用線性模型與決策樹模型作為局部的可解釋模型。
值得一提的是,由于近似模型的訓練使用隨機生成的擾動數據,模型的預測結果以及特征排序也會出現一定的隨機性。我們仍然考慮上文中姿態識別模型的 query point,使用線性模型對該點做近似分析,具體代碼及結果如下:
limeObj= lime(model, humanActivityData, 'QueryPoint',queryPt,'NumImportantPredictors',6);
f =plot(limeObj);
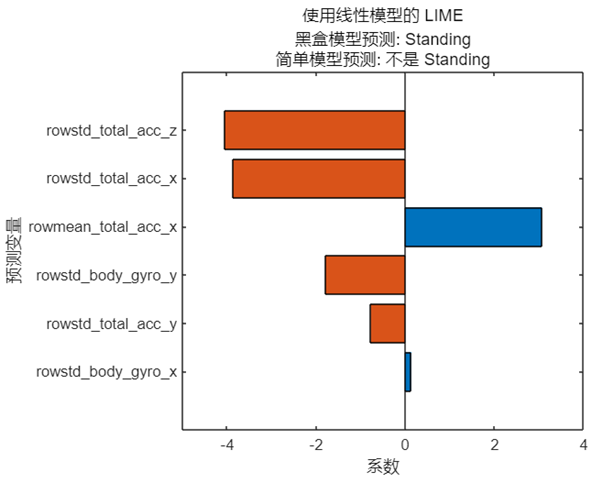
由于是線性模型,預測結果只是簡單地給出是否為 ‘Standing’,而橫坐標反映的是線性模型中每個特征對應的系數。一個有趣的現象是簡單模型的預測結果與黑盒模型的預測結果并不相同,這是否意味著這樣的結果是無效的、甚至是錯誤的?
我們先來選擇 rowstd_total_accd_z 與 towmean_total_acc_x,即系數正值和負值中絕對值最大的兩個特征(對應在數據中的位置為 9 和 1),采用上文中介紹的方法分別繪制 PDP,我們將 ‘Sitting’ 和 ‘Standing’ 兩個類別的曲線繪制在一張圖中,結果如下:
plotPartialDependence(model,9,{'Sitting','Standing'},humanActivityDataTest)
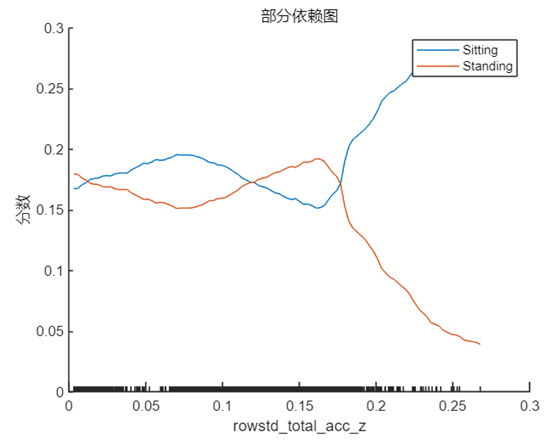
plotPartialDependence(model,1,{'Sitting','Standing'},humanActivityDataTest);
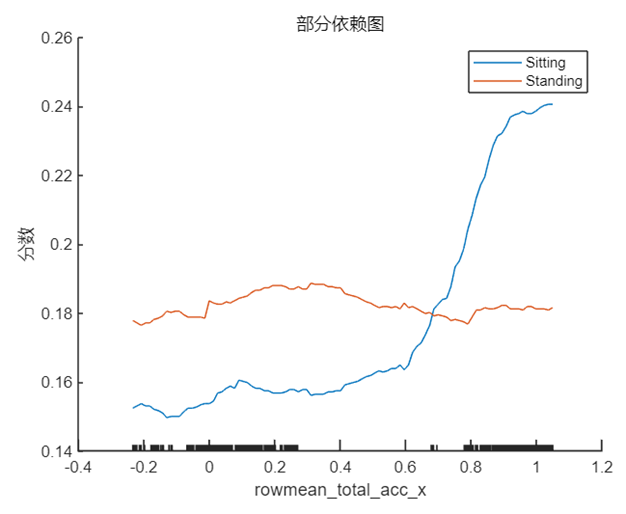
這兩個特征分別代表 z 方向加速度的標準差與 x 方向加速度的均值,結合第 1 節中其在該樣本點的實際取值 rowstd_total_acc_z=0.0048 以及 rowmean_total_acc_x=1.0129 可以看出,1.0129 對于模型做出正確預測會起到十分積極的作用,這可能也是簡單模型能夠做出不是 ‘Standing’ 的原因,因為站立的姿態通常不會在 x 方向產生較大的加速度,與此同時簡單模型的 rowstd_total_acc_z 的系數雖然很大,但是取值較小,這意味著z方向加速度標準差較小,數據比較集中,從 PDP 中也能看出在該點對于 ‘Standing’ 和 ‘Sitting’ 的區分度并不高,要在數值增大之后才會對結果有較為顯著的影響。
需要說明的是,通過 LIME 得到的特征排序(或系數大小)和 Shapley 值得到的結果相差較大,部分原因是在 LIME 中基于隨機擾動生成的數據得到的模型和黑盒模型原本就存在一定差異,可以嘗試使用不同的隨機數或使用其他簡單模型來得到多樣化的結果進行對比分析。
回到剛才的問題,這樣的簡單模型是否是無效的?其實機器學習的模型預測本身是一個十分復雜的過程,這是與黑盒模型強大的功能分不開的,無論是哪種解釋方法,目的都是幫助我們窺探預測的機理,從某一個角度理解分析產生這樣結果的原因,這些不同的角度相結合可以讓我們逐漸接近一個更加全面的分析結果,因此都是有意義的。
而 LIME 方法本身具備的隨機性以及簡單模型算法的選擇也給了我們更多可能性來進行不同的嘗試,關于 LIME 的使用可以參考之前的文章了解更多:如何信任機器學習模型的預測結果?(上)與 如何信任機器學習模型的預測結果?(下)。
后續工作
獲得模型的解釋結果只是第一步,在得到以上分析結果之后我們接下來可以做些什么呢?
現在我們已經知道 rowmean_body_gyro_z, rowstd_total_acc_z 等幾個特征對錯誤的分類結果有較大影響,我們可以進一步從原始數據分析更深層次的原因,比如我們采集的這個樣本點的數據是否有誤差?如果原始數據沒問題,那么求平均值或標準差的特征提取方式是否合適?是否應該選擇更加復雜的統計方式獲取特征?在模型的訓練階段是否可以通過修改代價函數等手段提高預測準確率?
顯然通過對一個樣本的分析,就得出關于整個模型的結論是不嚴謹的。以上分析結果提供給了我們一些思路和線索,我們可以對更多樣本點做類似分析,再結合其他手段去做下一步的改進。
采用類似的方法,我們還可以對判斷正確的樣本進行可解釋性的分析,來和我們對該問題的先驗知識進行對比,從而驗證模型是否正確。
其他方法
上文中通過實例介紹了幾種不同的可解釋性方法,除此之外 MATLAB 還支持與 PDP 類似、但是會將單個預測結果進行繪制以體現結果分布的 ICE 圖,以及本身具備可解釋性的 Generalized Additive 等諸多方法,可以在我們的幫助文檔中了解更多信息。
而對于深度學習,同樣發展了很多類似的可解釋性的方法,深度學習被廣泛應用于圖像、語音、信號處理等領域,針對這類問題,在 MATLAB 中可以很方便地使用 Occlusion Sensitivity, GradCAM 和 Image LIME 等方法,由于篇幅限制,本文不做詳細展開。
?
審核編輯:湯梓紅
 電子發燒友App
電子發燒友App


































評論