機(jī)器學(xué)習(xí)的基本步驟及實(shí)現(xiàn)方式比較
機(jī)器學(xué)習(xí)(Machine Learning)是計(jì)算機(jī)科學(xué)與人工智能的重要分支領(lǐng)域,也是大數(shù)據(jù)時(shí)代的一個(gè)重要技術(shù)。機(jī)器學(xué)習(xí)的基本思路是模仿人類的學(xué)習(xí)行為過程,該技術(shù)主要采用的算法包括聚類、分類、決策樹、貝葉斯、神經(jīng)網(wǎng)絡(luò)、深度學(xué)習(xí)等。總體而言,機(jī)器學(xué)習(xí)是讓計(jì)算機(jī)在大量數(shù)據(jù)中尋找數(shù)據(jù)規(guī)律,并根據(jù)數(shù)據(jù)規(guī)律對(duì)未知或主要數(shù)據(jù)趨勢(shì)進(jìn)行最終預(yù)測(cè)。在機(jī)器學(xué)習(xí)中,機(jī)器學(xué)習(xí)的效率在很大程度上取決于它所提供的數(shù)據(jù)集,數(shù)據(jù)集的大小和豐富程度也決定了最終預(yù)測(cè)的結(jié)果質(zhì)量。目前在算力方面,量子計(jì)算能超越傳統(tǒng)二進(jìn)制的編碼系統(tǒng),利用量子的糾纏與疊加特性拓展其對(duì)大量數(shù)據(jù)的運(yùn)算處理能力,從而能得出更準(zhǔn)確的模型參數(shù)以解決一些或工業(yè)或網(wǎng)絡(luò)的現(xiàn)實(shí)問題。
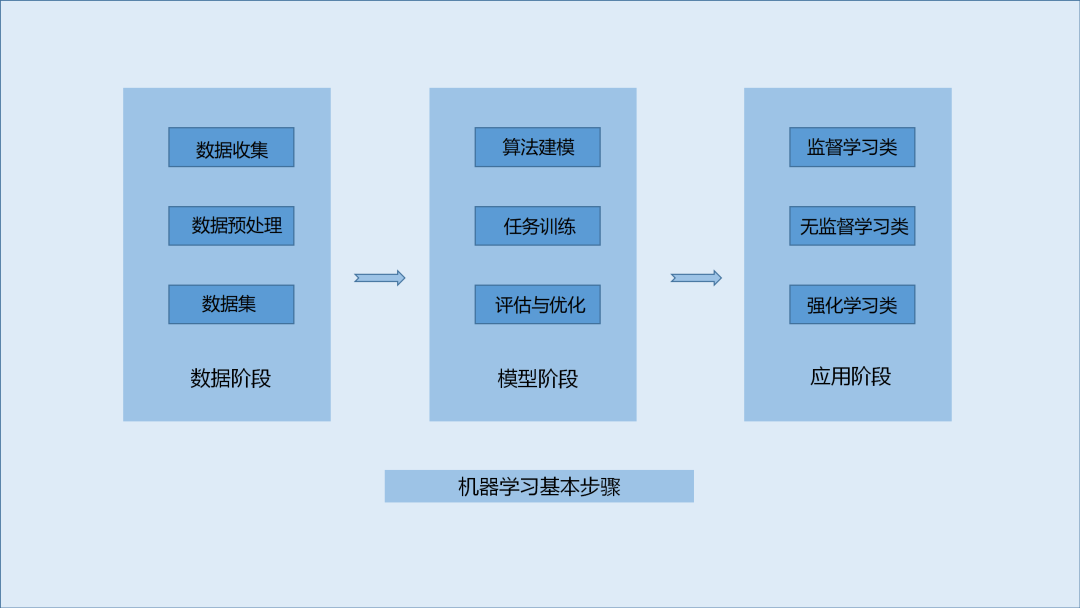
1.數(shù)據(jù)階段
1.1數(shù)據(jù)收集與預(yù)處理
互聯(lián)網(wǎng)時(shí)代,每分每秒中都有大量的數(shù)據(jù)信息產(chǎn)生。大量的數(shù)據(jù)如同養(yǎng)料一般,沒有源源不斷地?cái)?shù)據(jù)供應(yīng),以數(shù)據(jù)為基礎(chǔ)發(fā)展起來(lái)的各種技術(shù)如同無(wú)源之水缺少發(fā)展的活力。數(shù)據(jù)采集技術(shù)已經(jīng)有了階段性的發(fā)展,成熟度相對(duì)較高。因此,在提及機(jī)器學(xué)習(xí)、深度學(xué)習(xí)、自然語(yǔ)言處理等人工智能技術(shù)時(shí),數(shù)據(jù)采集常常被忽略。
數(shù)據(jù)采集技術(shù)也造就了許多以采集數(shù)據(jù)為主要業(yè)務(wù)的產(chǎn)品與應(yīng)用,如作為Hadoop的組件的Flume、開源的數(shù)據(jù)收集架構(gòu)Fluentd、Python的爬蟲架構(gòu)Scrapy等。還有一些數(shù)據(jù)收集服務(wù)平臺(tái)如百度統(tǒng)計(jì)、阿里云、大數(shù)據(jù)采集工具八爪魚。
盡管數(shù)據(jù)時(shí)代不缺少數(shù)據(jù),但有價(jià)值信息的數(shù)據(jù)即有效數(shù)據(jù)還需要對(duì)大量無(wú)序的數(shù)據(jù)進(jìn)行數(shù)據(jù)預(yù)處理。未經(jīng)過數(shù)據(jù)處理的數(shù)據(jù)往往存在以下問題:
數(shù)據(jù)不完整:缺少屬性值或僅僅包含聚集數(shù)據(jù);
數(shù)據(jù)含噪聲:大量數(shù)據(jù)中包含錯(cuò)誤或偏離期望的離群值;
數(shù)據(jù)標(biāo)簽規(guī)則不一:對(duì)于數(shù)據(jù)的分類規(guī)則與標(biāo)準(zhǔn)不一致,導(dǎo)致最終收集的數(shù)據(jù)不屬于同類數(shù)據(jù)。
數(shù)據(jù)預(yù)處理的方法主要有以下幾種:
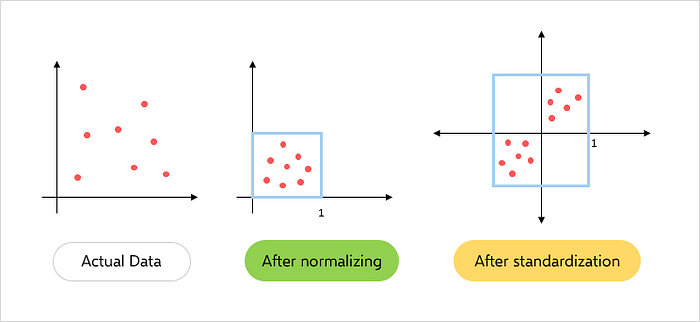
數(shù)據(jù)清洗:對(duì)數(shù)據(jù)進(jìn)行清洗,以去除噪聲、無(wú)關(guān)數(shù)據(jù)、完整性及其欠缺的數(shù)據(jù)、補(bǔ)充輕微缺損的數(shù)據(jù);
數(shù)據(jù)集成:數(shù)據(jù)集成多為數(shù)據(jù)分析的一個(gè)環(huán)節(jié),數(shù)據(jù)集成將多個(gè)數(shù)據(jù)源中的數(shù)據(jù)結(jié)合、存放在一個(gè)一致的數(shù)據(jù)存儲(chǔ),如數(shù)據(jù)倉(cāng)庫(kù)中,這些數(shù)據(jù)源可能包括多個(gè)數(shù)據(jù)庫(kù)、數(shù)據(jù)方或一般文件;
數(shù)據(jù)規(guī)約:數(shù)據(jù)歸約技術(shù)可以用來(lái)得到數(shù)據(jù)集的歸約表示,可以盡可能保持原數(shù)據(jù)的完整性,因而在歸約后的數(shù)據(jù)集上挖掘?qū)⒏行Вa(chǎn)生幾乎相同的分析結(jié)果。
1.2數(shù)據(jù)集準(zhǔn)備
數(shù)據(jù)集準(zhǔn)備是使用TensorFlow、Paddle Quantum等進(jìn)行機(jī)器學(xué)習(xí)的入門基礎(chǔ)。在實(shí)際練習(xí)或使用過程中,企業(yè)的數(shù)據(jù)相對(duì)而言獲取渠道固定、有較清晰的分類,因此在準(zhǔn)備數(shù)據(jù)集時(shí),做好分類后只需要將數(shù)據(jù)文件轉(zhuǎn)為機(jī)器學(xué)習(xí)可識(shí)別的文件即可。個(gè)人練習(xí)過程中,數(shù)據(jù)獲取難度較大,可參考KDnuggets上發(fā)表的一篇文章,作者總結(jié)了七十多個(gè)免費(fèi)的數(shù)據(jù)集(http://t.cn/RQJhwSi)。
經(jīng)處理后的數(shù)據(jù)制備為數(shù)據(jù)集。數(shù)據(jù)集一般可以分為訓(xùn)練集、驗(yàn)證集、測(cè)試集。其中,訓(xùn)練集主要用于訓(xùn)練模型;驗(yàn)證集主要用于選擇模型,通常在訓(xùn)練過程中使用訓(xùn)練集確定一些超參數(shù);測(cè)試集主要用于判斷網(wǎng)絡(luò)性能的好壞。
數(shù)據(jù)集的劃分方法一般也為三種,即留出法、交叉驗(yàn)證法、自助法。留出法是指將數(shù)據(jù)集 D 劃分成兩份互斥的數(shù)據(jù)集,一份作為訓(xùn)練集 S,一份作為測(cè)試集 T,在 S 上訓(xùn)練模型,在 T 上評(píng)估模型效果。留出法的優(yōu)點(diǎn)是簡(jiǎn)單好實(shí)現(xiàn),但訓(xùn)練集和測(cè)試集數(shù)據(jù)分布不一致時(shí)易引入偏差,最終影響數(shù)據(jù)模型評(píng)估結(jié)果。交叉驗(yàn)證法是將數(shù)據(jù)集D劃分為n個(gè)互斥的子集。然后每次選用一份數(shù)據(jù)子集作為測(cè)試集,其余的 n-1 份數(shù)據(jù)子集作為訓(xùn)練集,迭代n輪得到n個(gè)模型,最后將n次的評(píng)估結(jié)果匯總求平均值得到最終的評(píng)估結(jié)果。自助法使用有放回的重復(fù)采樣方式進(jìn)行訓(xùn)練集、測(cè)試集的構(gòu)建。自助采樣即確定所獲取的訓(xùn)練集樣本數(shù)n后,從數(shù)據(jù)集D中有放回的采樣n次,得到n條樣本的訓(xùn)練集,最后將未出現(xiàn)過的樣本作為測(cè)試集。
2.模型階段
2.1機(jī)器學(xué)習(xí)算法建模
機(jī)器學(xué)習(xí)可為監(jiān)督學(xué)習(xí)、無(wú)監(jiān)督學(xué)習(xí)和強(qiáng)化學(xué)習(xí)三類。監(jiān)督學(xué)習(xí)是指有標(biāo)簽數(shù)據(jù)、可進(jìn)行直接反闊并預(yù)測(cè)結(jié)果的一種學(xué)習(xí)方式,其主要目標(biāo)是從有標(biāo)簽的訓(xùn)練數(shù)據(jù)中學(xué)習(xí)模型,從而對(duì)未知的數(shù)據(jù)做出預(yù)測(cè)。無(wú)監(jiān)督學(xué)習(xí)是指數(shù)據(jù)沒有標(biāo)簽且數(shù)據(jù)結(jié)構(gòu)不明確或無(wú)數(shù)據(jù)結(jié)構(gòu)的。無(wú)監(jiān)督學(xué)習(xí)技術(shù)主要目的是在沒有已知結(jié)果變量或獎(jiǎng)勵(lì)函數(shù)的指導(dǎo)下,探索數(shù)據(jù)結(jié)構(gòu)、提取有價(jià)值的信息。強(qiáng)化學(xué)習(xí)的主要目的是開發(fā)一個(gè)系統(tǒng),然后通用該系統(tǒng)與環(huán)境之間發(fā)生交互產(chǎn)生的數(shù)據(jù)信息提高系統(tǒng)性能。強(qiáng)化學(xué)習(xí)(RL)分反饋是通過獎(jiǎng)勵(lì)函數(shù)對(duì)行動(dòng)度量的結(jié)果,常見的強(qiáng)化學(xué)習(xí)場(chǎng)景如國(guó)際象棋、制造機(jī)器人、管理生產(chǎn)規(guī)劃、企業(yè)決策、物流、電路設(shè)計(jì)、控制自動(dòng)駕駛汽車、控制無(wú)人機(jī)等等。
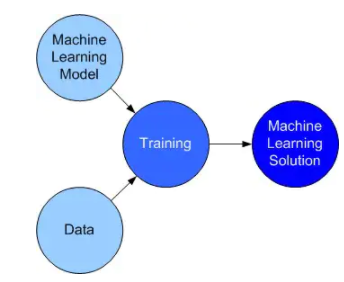
2.2模型訓(xùn)練
模型訓(xùn)練需要進(jìn)行多輪迭代,每輪迭代需要遍歷一次訓(xùn)練數(shù)據(jù)集并從中獲取小批量樣本。獲取樣本后將樣本數(shù)據(jù)輸入模型中得到預(yù)測(cè)值,對(duì)比預(yù)測(cè)值與真實(shí)值之間的損失函數(shù)(loss)。在得到損失函數(shù)以后,開始執(zhí)行梯度反向傳播并根據(jù)設(shè)置的優(yōu)化算法更新模型參數(shù)。最后模型的訓(xùn)練效果可通過損失函數(shù)值的變化來(lái)判斷,當(dāng)損失函數(shù)呈減小趨勢(shì),模型訓(xùn)練效果越顯著。以spam數(shù)據(jù)集為例:
將數(shù)據(jù)分為訓(xùn)練集和測(cè)試集并擬合模型
##codes from https://cloud.tencent.com/developer/article/1787782 library(caret) library(kernlab) data(spam) inTrain <- createDataPartition(y = spam$type, p = 0.75, list = FALSE) training <- spam[inTrain, ] testing <- spam[-inTrain, ] modelFit <- train(type ~., data = training, method="glm")
查看選項(xiàng):metric選項(xiàng)設(shè)置算法評(píng)價(jià),連續(xù)變量結(jié)果為均方根誤差RMSE;R^2^(從回歸模型獲得)分類變量結(jié)果為準(zhǔn)確性;Kappa系數(shù)(用于一致性檢驗(yàn),也可以用于衡量分類精度)
##codes from https://cloud.tencent.com/developer/article/1787782 args(train.default) function(x, y, method = "rf", preProcess = NULL, ..., weights = NULL, metric = ifelse(is.factor(y), "Accuracy", "RMSE"), maximize = ifelse(metric == "RMSE", FALSE, TRUE), trControl = trainControl(), tuneGrid = NULL, tuneLength = 3) NULL args(trainControl) function (method = "boot", number = ifelse(grepl("cv", method), 10, 25), repeats = ifelse(grepl("[d_]cv$", method), 1, NA), p = 0.75, search = "grid", initialWindow = NULL, horizon = 1, fixedWindow = TRUE, skip = 0, verboseIter = FALSE, returnData = TRUE, returnResamp = "final", savePredictions = FALSE, classProbs = FALSE, summaryFunction = defaultSummary, selectionFunction = "best", preProcOptions = list(thresh = 0.95, ICAcomp = 3, k = 5, freqCut = 95/5, uniqueCut = 10, cutoff = 0.9), sampling = NULL, index = NULL, indexOut = NULL, indexFinal = NULL, timingSamps = 0, predictionBounds = rep(FALSE, 2), seeds = NA, adaptive = list(min = 5, alpha = 0.05, method = "gls", complete = TRUE), trim = FALSE, allowParallel = TRUE) NULL
trainControl控制訓(xùn)練方法:設(shè)置重抽樣方法,boot:bootstrapping自舉法,boot632:調(diào)整的自舉法,cv:交叉驗(yàn)證 repeatedcv:重復(fù)交叉驗(yàn)證,LOOCV:留一交叉驗(yàn)證;number選項(xiàng)設(shè)置交叉驗(yàn)證或自舉重抽樣的次數(shù);repeats選項(xiàng)設(shè)置重復(fù)交叉驗(yàn)證的重復(fù)次數(shù);seed選項(xiàng)設(shè)置隨機(jī)數(shù)種子,可以設(shè)置全局隨機(jī)數(shù)種子,也可為每次重抽樣設(shè)置隨機(jī)數(shù)種子。
##codes from https://cloud.tencent.com/developer/article/1787782 set.seed(1235) modekFit2 <- train(type ~., data = training, method = "glm") modekFit2 Generalized Linear Model 3451 samples 57 predictor 2 classes: 'nonspam', 'spam' No pre-processing Resampling: Bootstrapped (25 reps) Summary of sample sizes: 3451, 3451, 3451, 3451, 3451, 3451, ... Resampling results: Accuracy Kappa 0.9156324 0.8229977
2.3模型評(píng)估與優(yōu)化
在機(jī)器學(xué)習(xí)的算法模型中,參數(shù)包括兩類分別為模型參數(shù)和超參數(shù)。其中模型參數(shù)不能人為預(yù)先設(shè)置,而是通過模型訓(xùn)練過程中自動(dòng)生成與更新。另一類參數(shù)為超參數(shù)。超參數(shù)在模型訓(xùn)練之前就可認(rèn)為設(shè)定,是控制模型結(jié)構(gòu)、功能、效率的一個(gè)調(diào)節(jié)入口。模型訓(xùn)練過程中產(chǎn)生的損失函數(shù)是進(jìn)行模型評(píng)估的一個(gè)指標(biāo),在模型訓(xùn)練過程結(jié)束后,可根據(jù)得到的各指標(biāo)值對(duì)模型進(jìn)行評(píng)估與優(yōu)化。模型優(yōu)化中涉及到一個(gè)超參數(shù)概念,是指在建模時(shí)將一些與模型無(wú)關(guān)的未知量設(shè)置為固定參數(shù)。常見超參數(shù)有學(xué)習(xí)效率、迭代次數(shù)(epoches)、隱層數(shù)目、隱層單元數(shù)、激活函數(shù)、優(yōu)化器等。
2.4預(yù)測(cè)或推理
機(jī)器學(xué)習(xí)的預(yù)測(cè)即在模型中輸入一個(gè)預(yù)測(cè)值,通過模型計(jì)算可以得到對(duì)應(yīng)的輸出值,該值即為模型的預(yù)測(cè)結(jié)果。簡(jiǎn)單的模型如一般簡(jiǎn)單線性回歸y=kx+b。真實(shí)值分布在線性模型兩側(cè),輸入一個(gè)對(duì)應(yīng)的x值即得到一個(gè)對(duì)應(yīng)的y值。
3.SVM算法示例
SVM是一類有監(jiān)督的分類算法,該算法思想主要為:首先假設(shè)樣本空間上有兩類樣本點(diǎn),SVM算法核心是希望找到一個(gè)超平面將兩類樣本分開;在尋找劃分超平面時(shí)應(yīng)盡可能使得兩類樣本到超平面距離最短。
首先,導(dǎo)入依賴,準(zhǔn)備算法運(yùn)行環(huán)境
import qiskit import matplotlib.pyplot as plt import numpy as np from qiskit.ml.datasets import ad_hoc_data from qiskit import BasicAer from qiskit.aqua import QuantumInstance from qiskit.circuit.library import ZZFeatureMap from qiskit.aqua.algorithms import QSVM from qiskit.aqua.utils import split_dataset_to_data_and_labels, map_label_to_class_name
?
其次,加載并查看數(shù)據(jù)
feature_dim = 2
training_dataset_size = 20
testing_dataset_size = 10
random_seed = 10598
shot = 10000
sample_Total, training_input, test_input, class_labels = ad_hoc_data(training_size=training_dataset_size,
test_size=testing_dataset_size,
gap=0.3,
n=feature_dim,
plot_data=True)
datapoints, class_to_label = split_dataset_to_data_and_labels(test_input)
print(class_to_label)
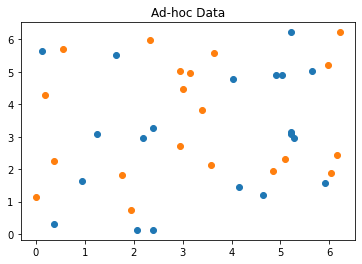
?
?
方式一:采用量子后端的方式運(yùn)行SVM算法
#getting my backend
backend = BasicAer.get_backend('qasm_simulator')
feature_map = ZZFeatureMap(feature_dim, reps=2)
svm = QSVM(feature_map,training_input,test_input,None)
svm.random_seed = random_seed
quantum_instance = QuantumInstance(backend,shots=shot,seed_simulator=random_seed, seed_transpiler=random_seed)
result = svm.run(quantum_instance)
打印訓(xùn)練中的核心矩陣
print("kernel matrix during the training:")
kernel_matrix = result['kernel_matrix_training']
img = plt.imshow(np.asmatrix(kernel_matrix),interpolation='nearest',origin='upper',cmap='bone_r')

?
?
獲得預(yù)測(cè)及其精度
predicted_labels = svm.predict(datapoints[0])
predicted_classes = map_label_to_class_name(predicted_labels,svm.label_to_class)
print('ground truth: {}'.format(datapoints[1]))
print('prediction: {}'.format(predicted_labels))
print('testing success ratio: ', result['testing_accuracy'])
輸出預(yù)測(cè)結(jié)果
ground truth: [0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1] prediction: [0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1] testing success ratio: 1.0
由以上輸出可看出,采用量子方式運(yùn)算SVM算法的精度結(jié)果為100%。
方式二:采用經(jīng)典方式運(yùn)行SVM算法
使用qiskit中的一個(gè)類似Scikit-learn實(shí)現(xiàn)
from qiskit.aqua.algorithms import SklearnSVM svm_classical = SklearnSVM(training_input, test_input) result_classical = svm_classical.run()
打印經(jīng)典方式訓(xùn)練中的kernel matrix
print("kernel matrix during the training:")
kernel_matrix_classical = result['kernel_matrix_training']
img = plt.imshow(np.asmatrix(kernel_matrix_classical),interpolation='nearest',origin='upper',cmap='bone_r')

?
?
打印預(yù)測(cè)結(jié)果及精度
predicted_labels_classical = svm_classical.predict(datapoints[0])
predicted_classes_classical = map_label_to_class_name(predicted_labels,svm.label_to_class)
print('ground truth: {}'.format(datapoints[1]))
print('prediction: {}'.format(predicted_labels_classical))
print('testing success ratio: ', result_classical['testing_accuracy'])
采用經(jīng)典方式的SVM算法輸出結(jié)果如下:
ground truth: [0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1] prediction: [1. 0. 0. 1. 0. 0. 0. 0. 1. 0. 1. 1. 1. 0. 0. 0. 0. 1. 1. 1.] testing success ratio: 0.65
由以上輸出可看出,采用經(jīng)典方式運(yùn)算SVM算法的精度結(jié)果為65%。
在SVM算法的分類中,尋找可劃分兩類樣本的超平面通常只能在更高維度上進(jìn)行,這就涉及到計(jì)算高維空間中的樣本點(diǎn)與平面之間的距離。因此,當(dāng)維度非常大時(shí),樣本點(diǎn)與超劃分平面的距離計(jì)算耗費(fèi)將很大。而內(nèi)核計(jì)算可以獲取數(shù)據(jù)點(diǎn)后返回一個(gè)距離,并可以通過優(yōu)化內(nèi)核使樣本點(diǎn)到超平面的距離最大化。這時(shí),量子計(jì)算的高效率的計(jì)算模式就體現(xiàn)出其優(yōu)越性,該示例在一定程度上說(shuō)明了QSVM優(yōu)于SVM。
編輯:黃飛
?
 電子發(fā)燒友App
電子發(fā)燒友App












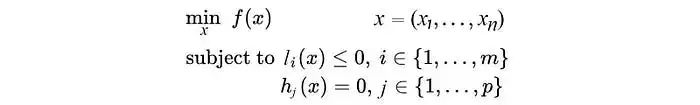










評(píng)論