哈夫曼樹的帶權路徑長度是什么？

　　1．樹的路徑長度

　　樹的路徑長度是從樹根到樹中每一結點的路徑長度之和。在結點數(shù)目相同的二叉樹中，完全二叉樹的路徑長度最短。

　　2．樹的帶權路徑長度（Weighted Path Length of Tree，簡記為WPL）

　　結點的權：在一些應用中，賦予樹中結點的一個有某種意義的實數(shù)。

　　結點的帶權路徑長度：結點到樹根之間的路徑長度與該結點上權的乘積。

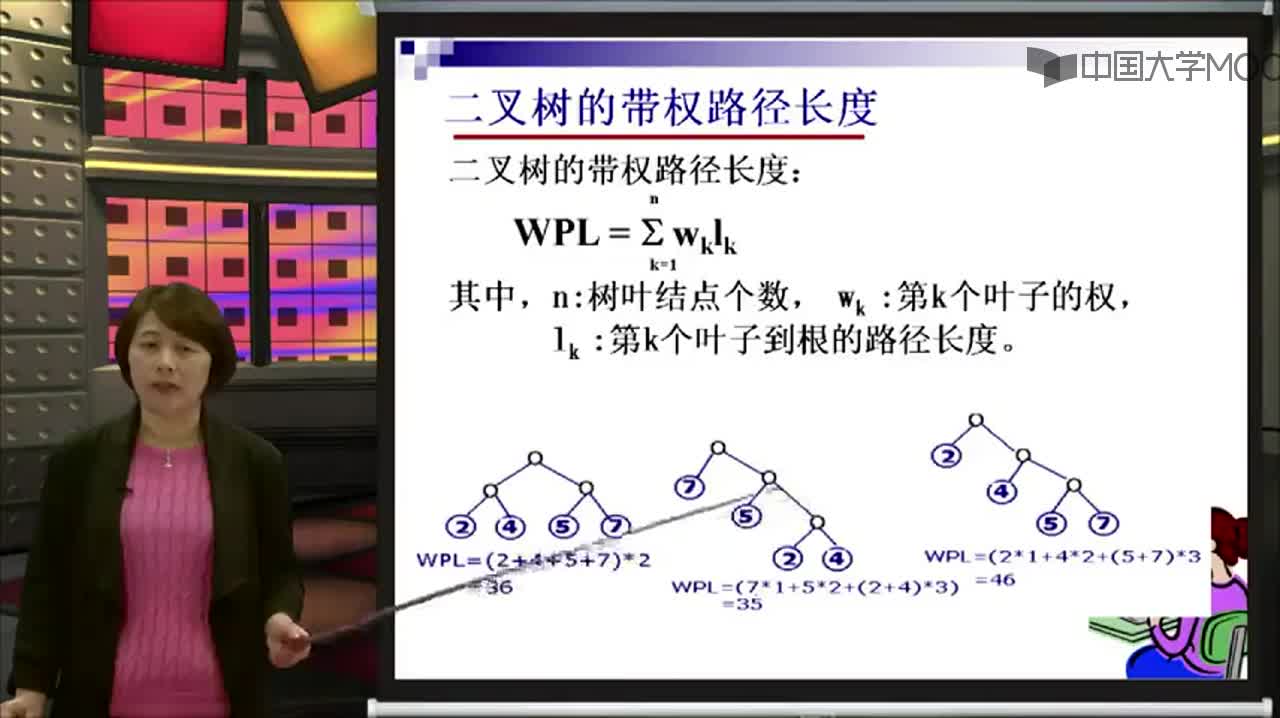
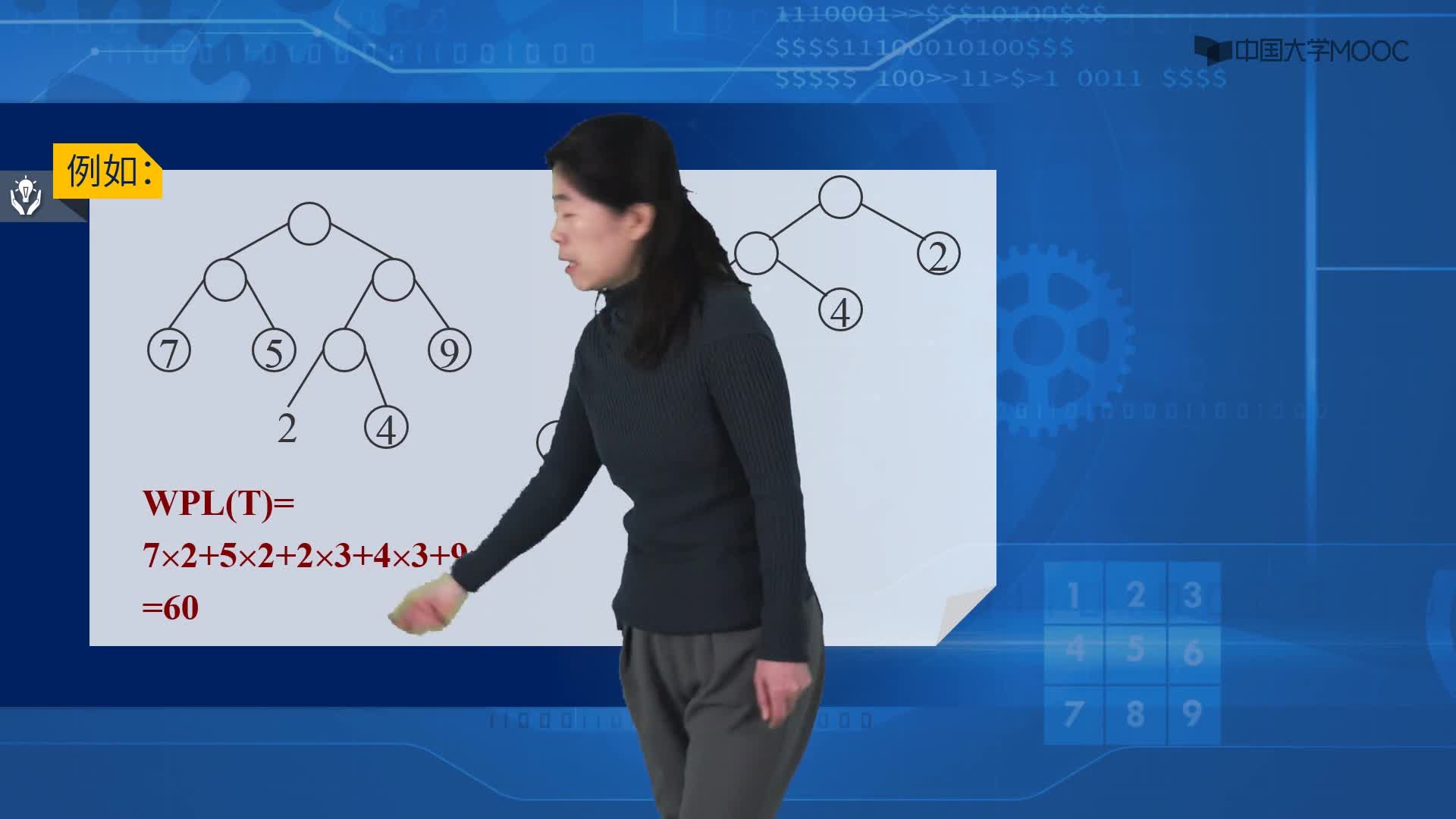
　　樹的帶權路徑長度（Weighted Path Length of Tree）：定義為樹中所有葉結點的帶權路徑長度之和，通常記為：

　　其中：

　　n表示葉子結點的數(shù)目

　　wi和li分別表示葉結點ki的權值和根到結點ki之間的路徑長度。

　　樹的帶權路徑長度亦稱為樹的代價。

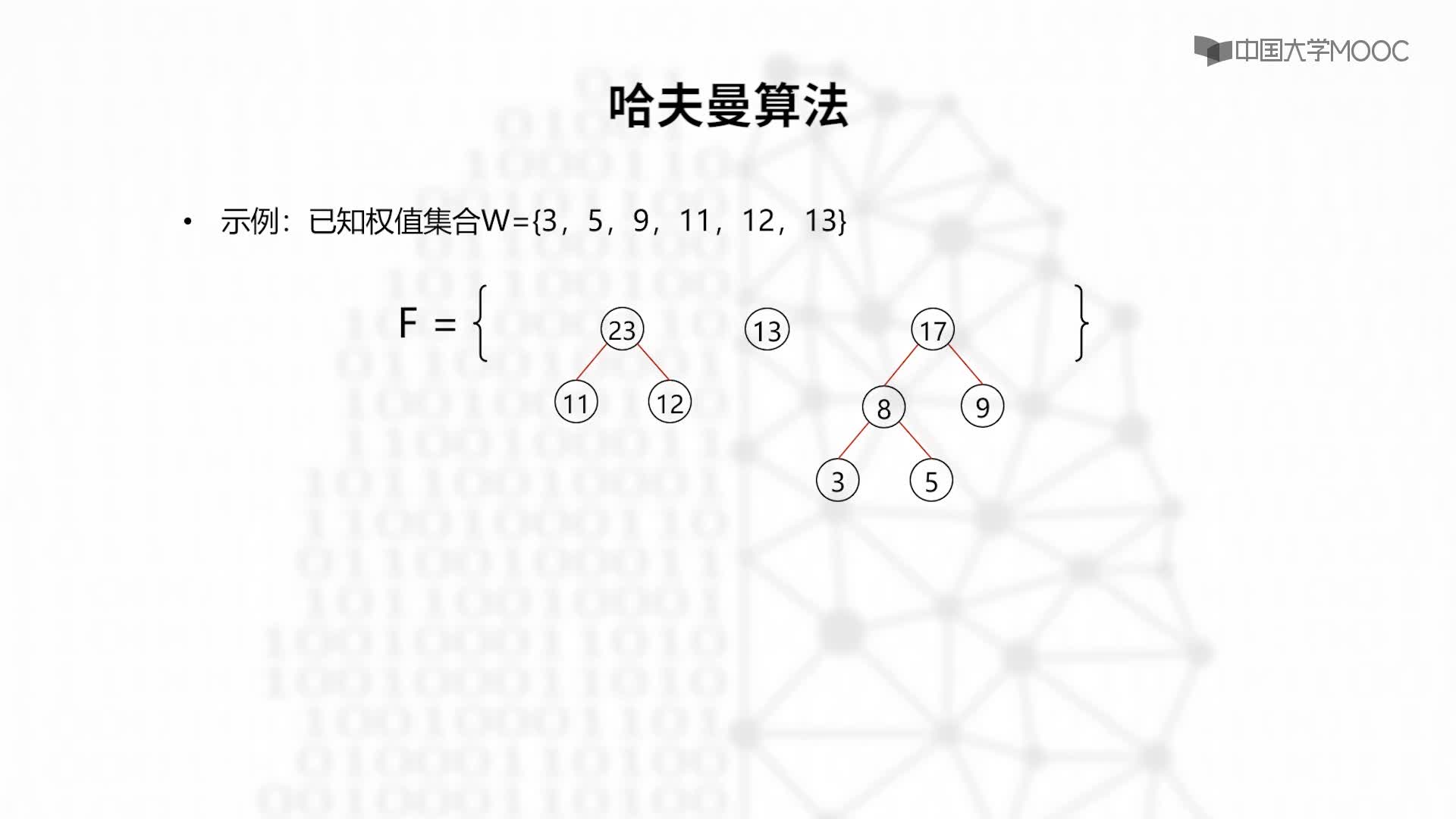
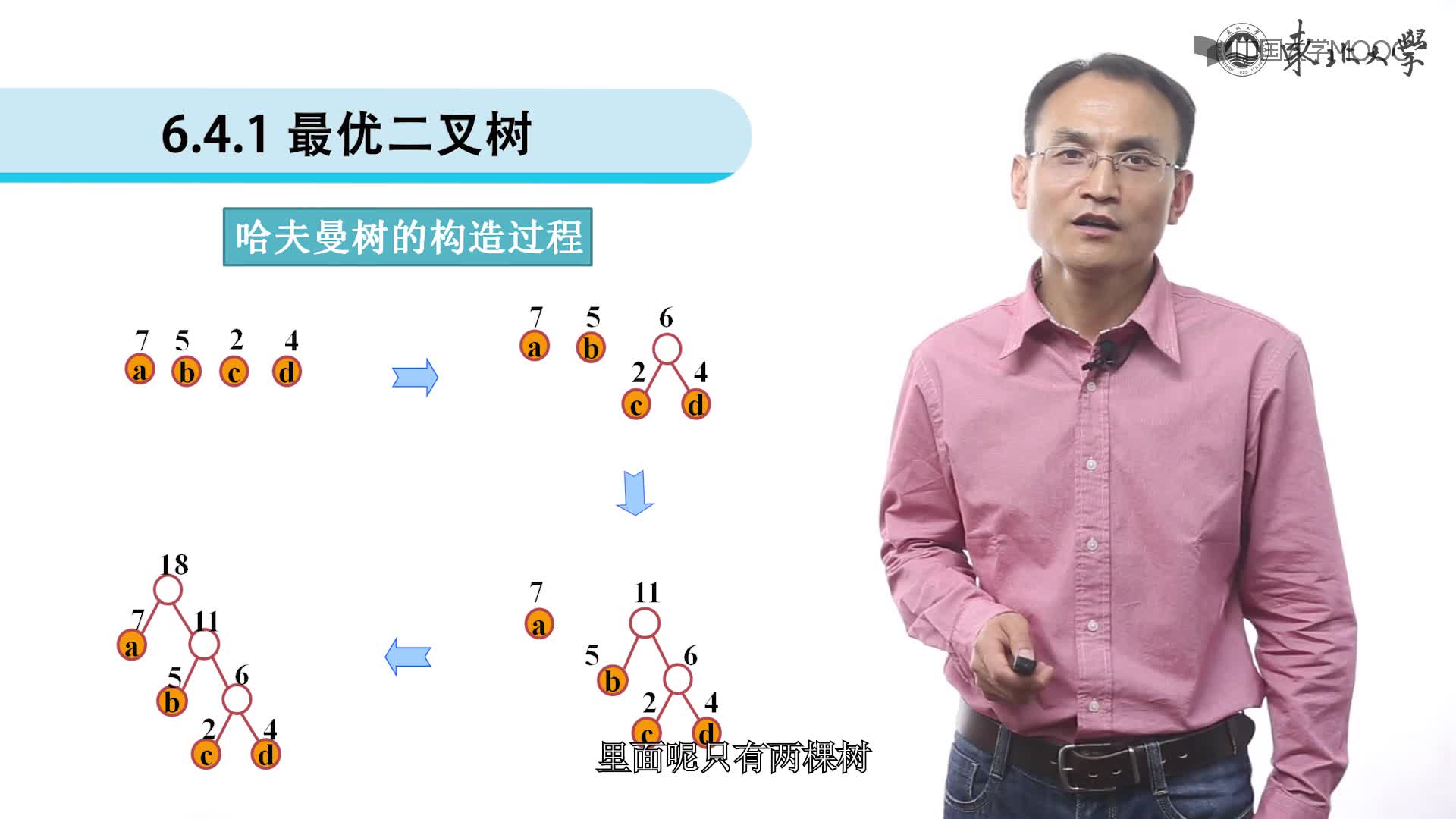
　　3．最優(yōu)二叉樹或哈夫曼樹

　　在權為wl，w2，…，wn的n個葉子所構成的所有二叉樹中，帶權路徑長度最小（即代價最小）的二叉樹稱為最優(yōu)二叉樹或哈夫曼樹。

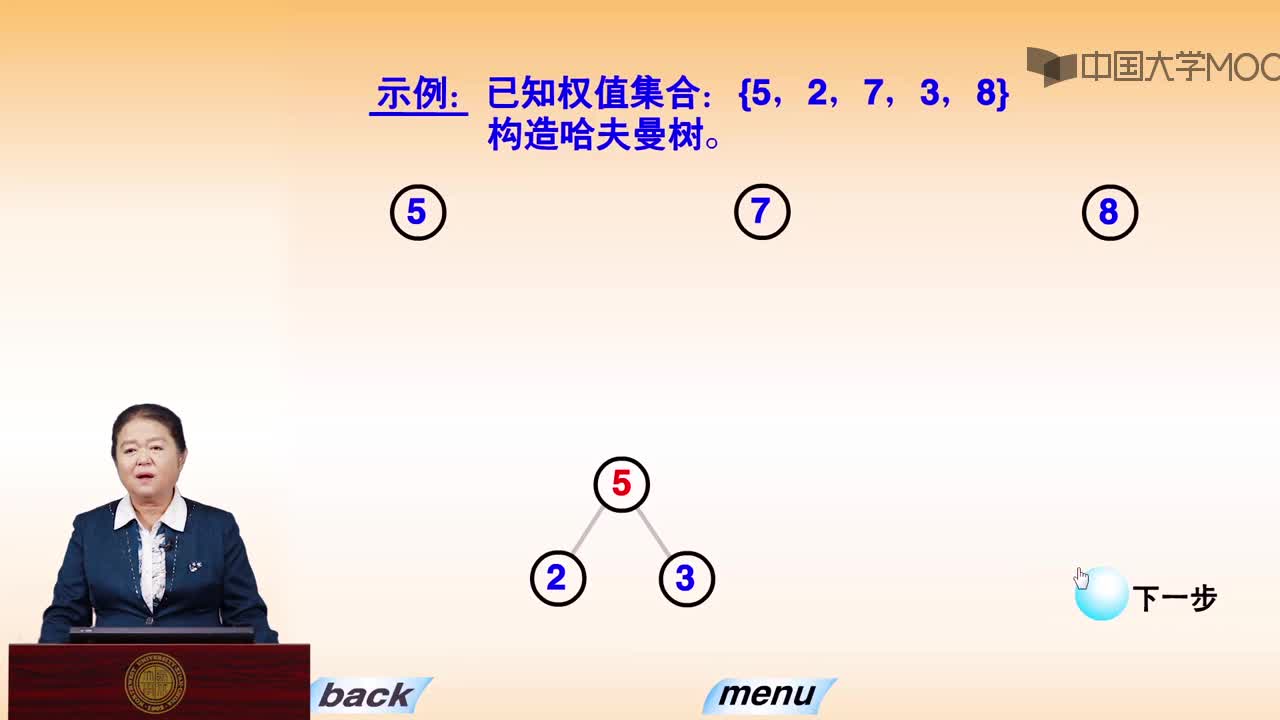
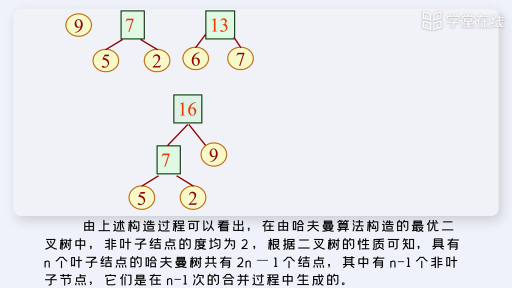
　　【例】給定4個葉子結點a，b，c和d，分別帶權7，5，2和4.構造如下圖所示的三棵二叉樹（還有許多棵），它們的帶權路徑長度分別為：

　　（a）WPL=7*2+5*2+2*2+4*2=36

　　（b）WPL=7*3+5*3+2*1+4*2=46

　　（c）WPL=7*1+5*2+2*3+4*3=35

　　其中（c）樹的WPL最小，可以驗證，它就是哈夫曼樹。

　　注意：

　　① 葉子上的權值均相同時，完全二叉樹一定是最優(yōu)二叉樹，否則完全二叉樹不一定是最優(yōu)二叉樹。

　　② 最優(yōu)二叉樹中，權越大的葉子離根越近。

　　③ 最優(yōu)二叉樹的形態(tài)不唯一，WPL最小

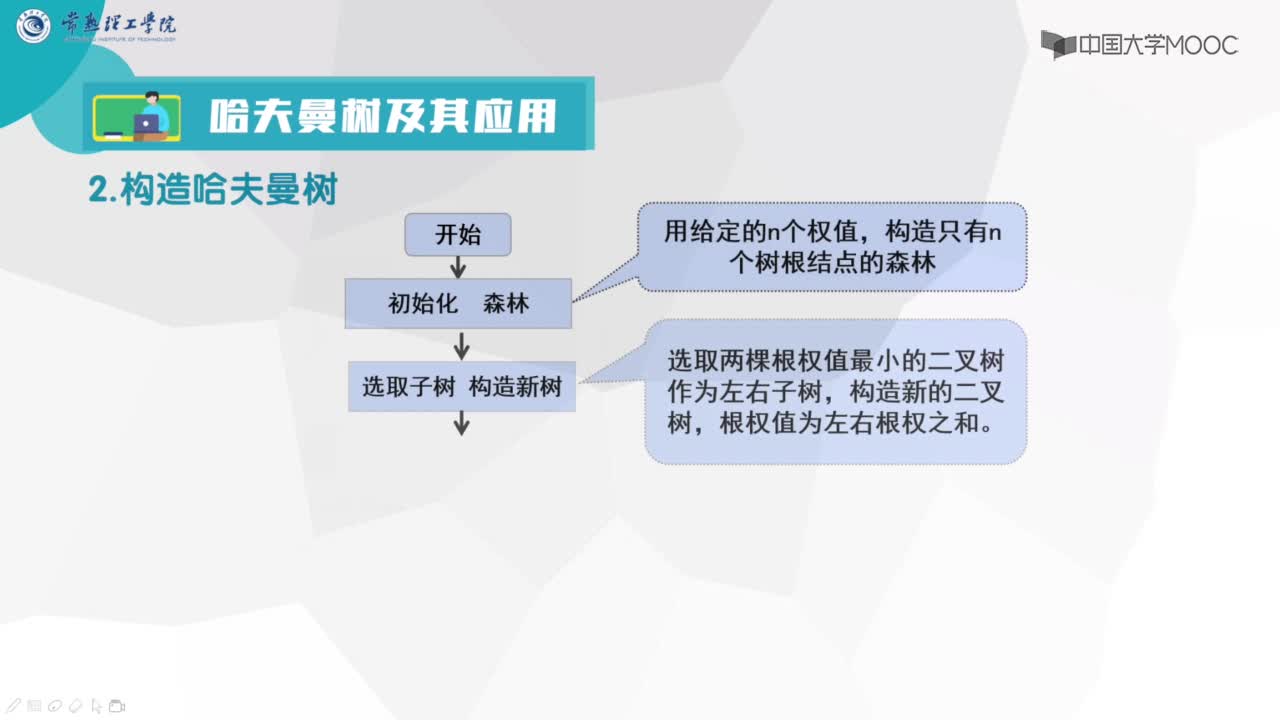
　　怎么求哈夫曼的帶權路徑長度

　　【問題描述】

　　已知輸入兩行正整數(shù)，第二行正整數(shù)之間用空格鍵分開，請建立一個哈夫曼樹，以輸入的數(shù)字為葉節(jié)點，求這棵哈夫曼樹的帶權路徑長度。

　　【輸入形式】

　　首先第一行為輸入正整數(shù)的個數(shù)，然后接下來的一行正整數(shù)，代表葉結點，正整數(shù)個數(shù)不超過1000個

　　【輸出形式】

　　輸出相應的權值

　　【樣例輸入】

　　5

　　4 5 6 7 8

　　【樣例輸出】

　　69

　　關于哈夫曼樹——

　　1、 路徑長度

　　從樹中一個結點到另一個結點之間的分支構成兩個結點之間的路徑，路徑上的分支數(shù)目稱做路徑長度。

　　1、 樹的路徑長度

　　路徑長度就是從樹根到每一結點的路徑長度之和。